Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
(Die Division durch Null ist schließlich nicht definiert.)
Merke dir:Niemals durch einen Term dividieren, der Null ergeben könnte!
Wenn du hier durch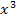 
teilen würdest, würdest du genau die Lösung verlieren, die du an sich suchst. Genau die x-Koordinate des gemeinsamen Punktes aller Funktionen der Schar erhältst du dann eben nicht mehr. Deshalb nicht durch 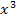dividieren, sondern folgendermaßen weiterrechnen:
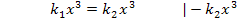
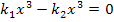
Als nächstes klammern wir 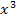auf der linken Seite der Gleichung aus.
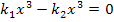
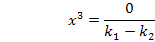
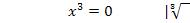
Weil die Lösung unabhängig vom Scharparameter ist, also weil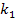 
und 
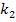bei der Lösung nicht mehr vorkommen, ist dies die x-Koordinate des Punktes P, der auf allen Graphen der Schar liegt. Es gibt auch keine weiteren (von k unabhängigen) Lösungen. Daher gibt es hier genau einen gemeinsamen Punkt aller Graphen der Schar.
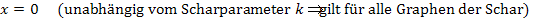
Die einzige Lösung enthält weder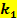 
noch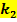 
und entspricht somit der x-Koordinate des gemeinsamen Punktes P aller Graphen der Schar.
Die y-Koordinate von P erhalten wir durch Einsetzen der berechneten x-Koordinate x = 0 in die Gleichung der Schar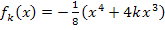 
. Damit der Punkt auf allen Graphen der Schar liegt, muss auch die y-Koordinate unabhängig sein von k. D.h. es darf auch in der y-Koordinate kein k mehr vorkommen. Wenn man oben richtig gerechnet hat, ist das allerdings automatisch der Fall. Sollte also bei dir die y-Koordinate des gemeinsamen Punktes aller Funktionen der Schar den Scharparameter noch enthalten, hast du dich sicher irgendwo verrechnet.
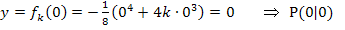
Der gemeinsame Punkt P aller Graphen der Schar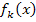 
ist also der Ursprung (0|0). Wirklich alle Graphen der Schar verlaufen durch diesen Punkt. Nur den Punkt P(0|0) haben sie alle gemeinsam. Damit ist der erste Teil der Teilaufgabe 4a.) gelöst.
Es muss aber noch gezeigt werden:
2. Alle Graphen der Schar haben im Punkt P die gleiche Steigung.
Im Punkt P(0|0) müssen alle Graphen der Schar 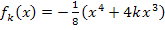die gleiche Steigung bzw. erste Ableitung besitzen. Die Ableitung an der Stelle x = 0 muss also einen Wert haben, der unabhängig ist von k. Anders formuliert: 
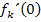muss eine richtige Zahl ohne k ergeben. Das ist nicht schwer zu beweisen. Wir leiten 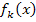einfach ab und setzen für x die Zahl Null ein. Im Endergebnis darf dann kein k mehr vorkommen.
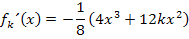
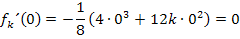
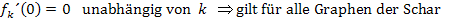
Alle Graphen der Schar 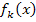haben demnach im Punkt P(0|0) die Steigung 0. Sie haben dort alle die gleiche Tangente. Deshalb berühren sie sich alle im Punkt P.
Zu 4b.)
Geg.: 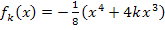mit der Definitionsmenge 
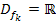und 
