Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
So, jetzt weißt du, was du nicht machen darfst, wenn du nachweisen sollst, dass es genau einen Punkt gibt, der auf allen Graphen der gegebenen Schar 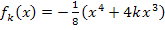 liegt. Doch wie lässt sich die Aufgabe nun lösen?
liegt. Doch wie lässt sich die Aufgabe nun lösen?
Wir müssen festlegen: 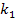 und
und 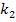 sind zwei beliebige, aber verschiedene Werte von k, mathematisch geschrieben:
sind zwei beliebige, aber verschiedene Werte von k, mathematisch geschrieben: 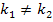
Dann sind 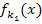 und
und 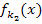 sicher zwei verschiedene Funktionen der Schar.
sicher zwei verschiedene Funktionen der Schar.
Es soll gezeigt werden:
1. Alle Graphen der Schar haben genau einen gemeinsamen Punkt P.
Allgemeiner Ansatz zur Ermittlung des gemeinsamen Punktes:

Um die x-Koordinaten der gemeinsamen Punkte von 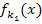 und
und 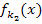 zu berechnen, müssen wir
zu berechnen, müssen wir 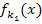 und
und 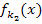 gleichsetzen. Dadurch bekommen wir eine Gleichung mit drei Buchstaben:
gleichsetzen. Dadurch bekommen wir eine Gleichung mit drei Buchstaben: 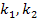 und x. Die Gleichung muss nach der Variablen, also nach x aufgelöst werden.
und x. Die Gleichung muss nach der Variablen, also nach x aufgelöst werden.
Dabei kommt es nicht nur auf die Anzahl der Lösungen an, sondern auch auf die Art der jeweiligen Lösung. Eine Lösung dieser Gleichung kann entweder abhängig sein von den Scharparametern 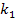 und
und 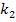 (d.h.
(d.h. 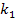 und
und 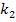 kommen in der Lösung noch vor) oder die jeweilige Lösung ist unabhängig vom Scharparameter (d.h.
kommen in der Lösung noch vor) oder die jeweilige Lösung ist unabhängig vom Scharparameter (d.h. 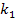 und
und 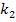 sind beide vollständig herausgefallen). Nur wenn eine Lösung weder
sind beide vollständig herausgefallen). Nur wenn eine Lösung weder 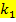 noch
noch 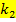 enthält, also wenn es sich um eine ganz normale Zahl ohne Scharparameter handelt, gilt sie für alle Funktionen der Schar. Eine Lösung, die dagegen
enthält, also wenn es sich um eine ganz normale Zahl ohne Scharparameter handelt, gilt sie für alle Funktionen der Schar. Eine Lösung, die dagegen 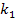 und
und 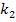 noch enthält, stellt bloßdie x-Koordinate des gemeinsamen Punktes von zwei bestimmten Funktionen der Schar dar, aber nicht von allen Graphen der Schar.
noch enthält, stellt bloßdie x-Koordinate des gemeinsamen Punktes von zwei bestimmten Funktionen der Schar dar, aber nicht von allen Graphen der Schar.
Es soll hier gezeigt werden, dass es genau einen gemeinsamen Punkt aller Funktionen der Schar 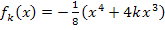 gibt. Es muss sich in diesem Beispiel also genau eine Lösung ergeben, die unabhängig ist von
gibt. Es muss sich in diesem Beispiel also genau eine Lösung ergeben, die unabhängig ist von 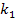 und
und 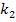 . D.h. es darf weder
. D.h. es darf weder 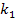 noch
noch 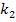 in dieser Lösung vorkommen;diese eine Lösung muss eine richtige Zahl ohne
in dieser Lösung vorkommen;diese eine Lösung muss eine richtige Zahl ohne 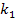 und
und 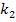 sein.
sein.
Ob sich außerdem noch weitere Lösungen ergeben, die abhängig sind von 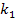 und
und 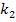 , kann man im Vorhinein nicht sagen. Das hängt davon ab, ob sich jeweils zwei Graphen der Schar nur in einem Punkt oder in mehreren Punkten schneiden bzw. berühren. Auf jeden Fall muss hier genau eine Lösung herauskommen, bei der weder
, kann man im Vorhinein nicht sagen. Das hängt davon ab, ob sich jeweils zwei Graphen der Schar nur in einem Punkt oder in mehreren Punkten schneiden bzw. berühren. Auf jeden Fall muss hier genau eine Lösung herauskommen, bei der weder 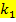 noch
noch 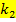 enthalten ist.
enthalten ist.
So, jetzt geht es endlich los mit der Rechnung.
Bitte unbedingt hinschreiben!
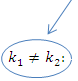
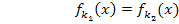
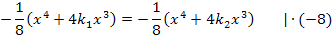
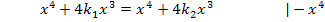
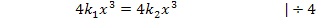
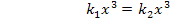
Was würdest du jetzt als nächstes machen? Bitte, erst selbst überlegen!
Vielleicht bist du auf die Idee gekommen, durch 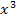 zu teilen. Dann bist du genau in die Falle getappt! An dieser Stelle darfst du nämlich keinesfalls durch
zu teilen. Dann bist du genau in die Falle getappt! An dieser Stelle darfst du nämlich keinesfalls durch 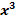 dividieren, denn
dividieren, denn 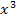 könnte schließlich Null ergeben und durch Null darf man nicht teilen!
könnte schließlich Null ergeben und durch Null darf man nicht teilen!

