Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Woher wüsstest du dann, welcher der beiden Punkte wirklich auf allen Graphen der Schar liegt und nicht bloßauf genau diesen beiden speziellen Graphen der Schar? Deshalb darfst du hier keine konkreten Werte für k einsetzen.
Damit dir wirklich klar wird, warum du nicht einfach zwei konkrete Funktionen der Schar miteinander schneiden darfst, wenn du den gemeinsamen Punkt aller Graphen der Schar suchst, sind in der folgenden Abbildung einige Graphen einer anderen Schar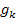 
dargestellt, an Hand derer sich die Problematik gut erklären lässt. (Die folgende Abbildung zeigt also nicht die Graphen der Schar 
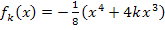aus dem Bsp. 4, sondern eine andere nicht näher bekannte Schar 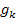. Die Graphen der Schar 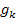werden im Folgenden mit 
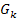bezeichnet.)
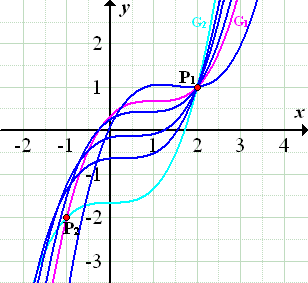
Abb.:Einige Graphen 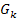einer nicht näher bekannten Schar 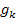, bei der es genau einen gemeinsamen Punkt aller Graphen der Schar gibt. Durch den Punkt 
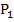verlaufen offensichtlich alle Graphen der Schar. Zwei Graphen der Schar 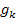sind in anderen Farben dargestellt. Es handelt sich dabei um den Graph 
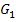zu k = 1 (in Rosa) und um den Graphen 
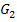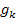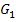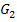zu k = 2 (in Hellblau). Diese beiden Graphen stellen zwei willkürlich gewählte konkrete Beispiele für Funktionen der Schar dar. Die Graphen und schneiden sich in den rot markierten Punkten 
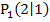und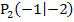 
. Der Punkt 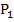liegt wirklich auf allen Graphen der Schar, wogegen der Punkt 
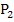nur auf den Graphen 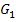und 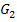liegt, nicht aber auf den anderen Graphen der Schar.
Stell dir jetzt vor, du hättest die Werte k = 1 und k = 2 gewählt. Wenn du die gemeinsamen Punkte dieser beiden konkreten Funktionen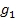 
und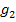 
der Schar 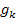ermittelt hättest, hättest du zwei verschiedene Lösungen erhalten. Es gibt schließlich zwei gemeinsame Punkte von 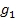und 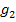, nämlich die Punkte 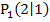und 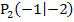. Aber nur der Punkt 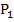ist tatsächlich der gemeinsame Punkt aller Graphen der Schar 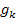. Der Punkt 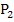ist dagegen nur Schnittpunkt von 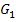und 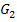, nicht aber von allen Graphen 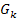. In der obigen Abbildung kannst du sehen, dass 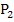nicht auf den anderen Graphen der Schar 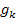liegt. Wenn du also willkürlich zwei konkrete Zahlen für k einsetzt und die beiden zugehörigen Funktionen der Schar gleichsetzt, bekommst du nicht heraus, welcher Punkt auf allen Graphen der Schar liegt, sondern nur die gemeinsamen Punkte der zwei ausgewählten Funktionen der Schar. Das hilft uns aber nicht weiter, wenn wir den gemeinsamen Punkt aller Graphen der Schar ermitteln sollen. Deshalb niemals konkrete Zahlen für den Scharparameter einsetzen, wenn es um alle Graphen der Schar geht.
