Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

a.) Zeige, dass alle Graphen 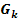der Funktionen 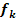genau einen gemeinsamen Punkt P besitzen, und dass sie sich dort alle berühren! Gib die Koordinaten dieses Punktes P an!

b.) Bestimme alle Nullstellen der Schar 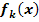in Abhängigkeit von k und gib jeweils ihre Vielfachheiten an!

c.) Für k <0 existieren zwei verschiedene Wendepunkte von 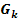. Berechne k so, dass die Wendetangente an 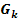im rechten Wendepunkt parallel zur Geraden 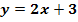verläuft. Berechne in Abhängigkeit von k und für den vorher ermittelten Wert von k auch die Art und Koordinaten der Wendepunkte.

d.) Berechne für k <0  die Gleichung der Kurve, auf der alle Wendepunkte der Schar liegen!

Lösung:

Zu 4a.)

Geg.: 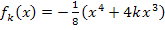mit der Definitionsmenge 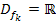und

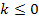
Zu zeigen ist, dass alle Graphen der Schar 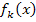genau einen gemeinsamen Punkt P besitzen und dass sich alle Graphen der Schar in diesem Punkt berühren (und nicht schneiden).

Hinweis:Zwei verschiedene Funktionen  berühren sich im Punkt P, wenn P auf beiden Funktionen liegt und zusätzlich beide Funktionen an dieser Stelle die gleiche Steigung haben. In anderen Worten:In einem Berührpunkt sind nicht nur die Funktionswerte (y-Koordinaten) der beiden Funktionen gleich, sondern auch die ersten Ableitungen (Steigungen) der zwei Funktionen.

Es müssen daher folgende zwei Dinge nachgewiesen werden:

1. Alle Graphen der Schar haben genau einen gemeinsamen Punkt P.

2. Alle Graphen der Schar haben im Punkt P die gleiche Steigung.

Wie kann man das nachweisen? Dir ist bestimmt klar, dass man zwei verschiedene Funktionen der Schar 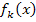erhält, indem man zwei verschiedene Werte für k einsetzt. Jetzt denkst du dir bestimmt:„Super, ich nehme einfach zwei konkrete verschiedene Zahlen und setze diese Zahlen bei 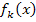für k ein. Dann kann ich diese beiden Funktionen der Schar miteinander gleichsetzen, um die x-Koordinaten der gemeinsamen Punkte beider Funktionen zu finden.“ Dadurch erhieltest du allerdings nur die x-Koordinaten der gemeinsamen Punkte genau dieser beiden konkreten Funktionen der Schar und nicht aller Funktionen der Schar.

Es ist an sich schon richtig, dass man zwei Funktionen gleichsetzen muss, wenn man die gemeinsamen Punkte der beiden Funktionen ermitteln will. Wir sollen hier aber nicht nur die gemeinsamen Punkte von zwei bestimmten Funktionen der Schar ermitteln, sondern von allen Funktionen der Schar. Es könnte nämlich zum Beispiel sein, dass  die zwei Funktionen der Schar, die du ausgewählt hast, zwei gemeinsame Punkte 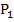und 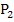 haben, dass aber nur der eine Punkt 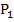auch auf allen anderen Funktionen der Schar liegt und der andere Punkt 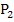eben nicht.

---