Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen

Es liegt also bei 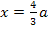ein Wendepunkt vor, egal was man für a einsetzt.

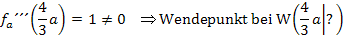
Berechnung der y-Koordinate des Wendepunktes:

Dazu setzen wir die x-Koordinate des Wendepunktes für x in 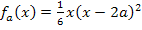ein.

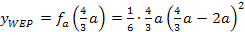
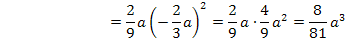
Der Wendepunkt hat also die Koordinaten: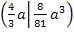

2. Schritt:Parameter a eliminieren

Aus den Koordinaten des Wendepunktes ergeben sich die beiden folgenden Gleichungen:

Beide Gleichungen enthalten den Parameter a. Deshalb müssen wir a eliminieren, indem wir Gleichung I. nach a auflösen und in Gleichung II. einsetzen.

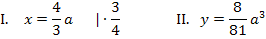
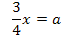
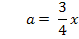
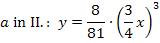
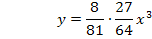
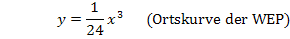
Damit haben wir die Gleichung der Ortskurve der Wendepunkte der Schar 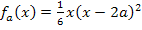aus dem Einführungsbeispiel nach der 1. Methode rechnerisch ermittelt.

Nun müssen wir uns noch die Definitionsmenge der Ortskurve überlegen:Wegen a >0 ist die x-Koordinaten 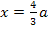der Wendepunkte immer positiv. Daher ist die Ortskurve der WEP nur für x >0 definiert.

Nun noch einmal mit der 2. Methode.

Lösung (nach der 2. Methode)

1. Schritt:x- Koordinate des Wendepunktes berechnen

Der Rechenweg, wie man die x-Koordinate des Wendepunktes berechnet, wurde oben bei der 1. Methode bereits gezeigt. (Siehe oben!)

Die x-Koordinate des Wendepunktes lautet:

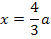
2. Schritt:Gleichung nach a auflösen und das Ergebnis für a in 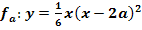einsetzen.

Auflösen nach a:

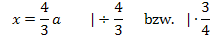
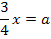
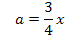
Ergebnis für a einsetzen in :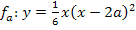

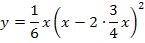
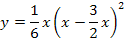
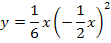
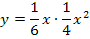
Es ergibt sich natürlich das gleiche Ergebnis wie schon oben bei der ersten Methode. Die Definitionsmenge der Ortskurve der WEP haben wir uns schon bei der ersten Methode überlegt:Die Ortskurve 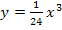ist wegen a >0 ausschließlich für x >0 definiert. Die x-Koordinaten 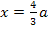der Wendepunkte kann wegen a >0 schließlich nur positive Werte annehmen. Daher darf die Ortskurve nur für x >0 (also rechts von der y-Achse) gezeichnet werden.

Du kannst die Ortskurve der Wendepunkte mit einigen ausgewählten Graphen der Schar in der nachfolgenden Abbildung sehen.

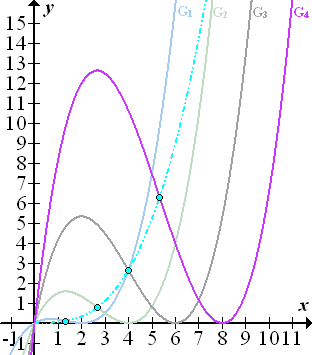
Abb.:Einige Graphen der Schar 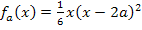mit x ℝ und die Ortskurve der Wendepunkte 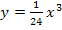(hellblau gestrichpunkted) mit x >0

Nun müsste dir die Vorgehensweise bei der Berechnung einer Ortskurve an sich klar sein. Damit du das Verfahren selbst noch öfter üben und direkt mit der Lösung vergleichen kannst, wird in den folgenden Beispielaufgaben unter anderem auch immer wieder mal eine Ortskurve vorkommen. Doch gibt es noch viele weitere interessante Fragestellungen rund um das Thema Funktionenscharen. Dazu mehr im nächsten Beispiel.

4. Bsp.:

Gegeben sind die reellen Funktionen 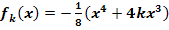mit der Definitionsmenge 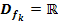und 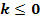. Der Graph einer Funktion 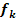dieser Schar wird mit 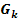bezeichnet.

---