Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Dazu setzen wir einfach die Koordinaten des Punktes P in die Gleichung der Schar ein. So erhalten wir eine Gleichung, die nur noch a als Unbekannte enthält. Wenn man die Gleichung nach a auflöst, erhält man die gesuchten Werte.
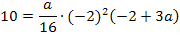
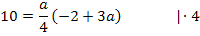
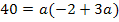
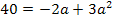
Es handelt sich um eine gemischtquadratische Gleichung, d.h. eine Gleichung mit der Unbekannten zum Quadrat und der Unbekannten ohne Potenz. Solche Gleichungen lassen sich lösen, indem man sie nach Null umstellt. Wir müssen also alles auf eine Seite der Gleichung bringen. Danach lässt sich die Mitternachtsformel anwenden.
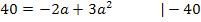
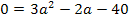
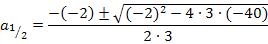
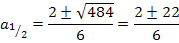
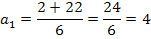
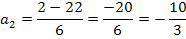
Für die Werte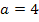 
und 
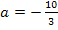liegt der Punkt 
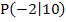auf dem Graphen der Schar.
Zu 1b.)
Geg.: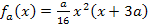 
mit 
Gesucht ist diejenige Funktion der Schar, deren Graph bei x = 4 eine waagrechte Tangente besitzt. Das bedeutet, dass wir zuerst den Parameter a berechnen müssen, für den die Bedingung „waagrechte Tangente bei x = 4“ erfüllt ist. Diesen Wert von a muss man dann noch in die Gleichung von 
einsetzen. Das ergibt die gesuchte Funktion.
Eine waagrechte Tangente hat bekanntlich die Steigung Null. Daher muss die gesuchte Funktion der Schar an der Stelle x = 4 die Steigung Null haben. Die Steigung einer Funktion entspricht ihrer ersten Ableitung. Deshalb muss gelten:
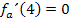
Wir bilden nun erst einmal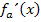 
. Anschließend setzen wir dann für x die Zahl 4 ein und setzen das Ganze gleich Null. Dadurch ergibt sich eine Gleichung, die nur noch a als Unbekannte enthält. Wenn man die Gleichung nach a auflöst, erhält man den gesuchten Wert von a.
Vorsicht:Zuerst 
bei 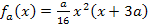in die Klammer hineinmultiplizieren, dann erst ableiten! Wenn man nämlich vor dem Ableiten nicht ausmultipliziert, müsste man beim Ableiten Die Produktregel anwenden, weil es sich bei 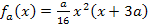um ein Produkt handelt, das in beiden Faktoren die Variable x enthält. Das Ableiten mit der Produktregel wäre aber viel zu umständlich. Den Faktor 
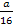musst du nicht unbedingt in die Klammer hineinmultiplizieren. Er kann außerhalb der Klammer stehen bleiben, denn 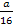enthält schließlich kein x und ist somit bloßeine multiplikative Konstante (d.h. quasi eine Zahl, mit der multipliziert wird). Multiplikative Konstanten werden beim Ableiten einfach abgeschrieben;deshalb muss der Faktor 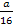vor dem Ableiten nicht mit dem in die Klammer hineinmultipliziert werden. Wir lassen hier den Faktor 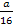deshalb außerhalb der Klammer stehen und multiplizieren bloßdas in die Klammer hinein, dann leiten wir die Funktion in dieser Form ab.
