Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
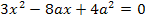
Diese Gleichung muss nach x aufgelöst werden. Weil in der Gleichung sowohl 
als auch x ohne Potenz und ein Ausdruck ohne x (eine Konstante) vorkommt, verwenden wir die Mitternachtsformel.
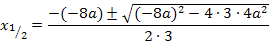
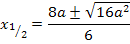
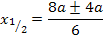
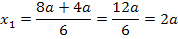
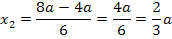
Jetzt müssen wir herausfinden, welche der beiden berechneten x-Koordinaten zum relativen Hochpunkt der Schar gehört. Wir verwenden hier die Zweite Ableitung f´´(x), um das herauszufinden. (Du kannst stattdessen auch die Monotonie von 
untersuchen, das ist aber umständlicher.) Wir ermitteln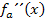 
und setzen nacheinander die ermittelten x-Koordinaten in 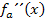ein. Wo ein Hochpunkt vorliegt, muss der Graph rechtsgekrümmt sein, d.h. es muss bei der zweiten Ableitung etwas Negatives herauskommen.
Die erste Ableitung lautet:
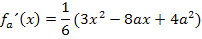
Daraus folgt für die zweite Ableitung:
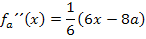
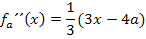
Nun setzen wir die ermittelten x-Koordinaten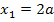 
und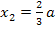 
in die zweite Ableitung ein und ermitteln die Vorzeichen der Ergebnisse für a >0.
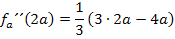
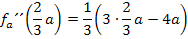
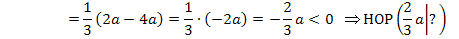
Nun kennen wir die x-Koordinate des Hochpunktes in Abhängigkeit von a. Sie lautet:
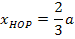
Als nächstes berechnen wir die zugehörige y-Koordinate. Dazu setzen wir die berechnete x-Koordinate des Hochpunktes für x in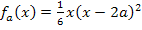 
ein. (Die y-Koordinate des Tiefpunktes berechnen wir hier nicht, weil die Koordinaten der Tiefpunkte für die Ortskurve der Hochpunkte nicht von Belang sind.)
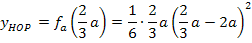
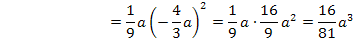
Der Hochpunkt hat also die Koordinaten: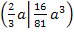 
2. Schritt:Parameter a eliminieren
Aus den Koordinaten des Hochpunktes ergeben sich die beiden folgenden Gleichungen:
Beide Gleichungen enthalten den Parameter a. Deshalb müssen wir a eliminieren, indem wir Gleichung I. nach a auflösen und in Gleichung II. einsetzen.
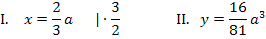
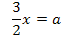
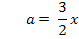
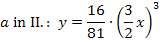
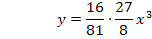
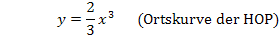
Damit haben wir die Gleichung der Ortskurve der relativen Hochpunkte der Schar 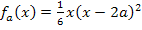aus dem Einführungsbeispiel nach der 1. Methode rechnerisch ermittelt.
Nun noch einmal mit der 2. Methode.
Lösung (nach der 2. Methode)
1. Schritt:x- Koordinate des relativen Hochpunkts berechnen
Der Rechenweg, wie man die x-Koordinate des Hochpunktes berechnet, wurde oben bei der 1. Methode bereits gezeigt. (Siehe oben!)
Die x-Koordinate des relativen Hochpunktes lautet:
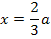
2. Schritt:Gleichung nach a auflösen und das Ergebnis für a in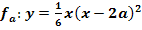 
einsetzen.
Auflösen nach a:
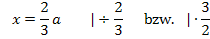
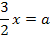
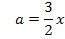
Ergebnis für a einsetzen in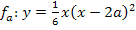 
:
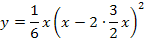
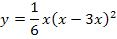
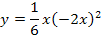
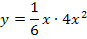
Es ergibt sich natürlich das gleiche Ergebnis wie schon oben bei der ersten Methode.
