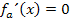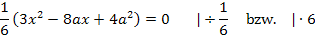Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Versuche doch jetzt gleich mal selbständig die Ortskurve der relativen Hochpunkte und die Ortskurve der Wendepunkte des Einführungsbeispiels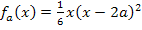 
zu berechnen! (Dies ist die Schar, an deren Beispiel der Begriff der Ortskurve anfangs erklärt wurde. Ganz am Anfang der Erklärungen zum Thema „Ortskurve“ wurden die Graphen einiger Funktionen dieser Schar für ein paar ausgewählte Werte von a gezeigt. In derselben Abbildung sind auch die Ortskurve ihrer relativen Hochpunkte und die Ortskurve ihrer Wendepunkte zu sehen. Siehe oben!) Du kannst jetzt selbst entscheiden, welche Methode für die Berechnung der Ortskurven dir persönlich am liebsten ist. Nur diese Methode verwendest du dann immer. Es werden im Folgenden jeweils beide Wege gezeigt, damit du deinen eigenen Lösungsweg auf jeden Fall damit vergleichen kannst, egal nach welcher Methode du vorgegangen bist.
Zum Einführungsbeispiel 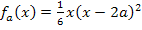mit a >0
a.) Gesucht:Ortskurve der relativen Hochpunkte (d.h. es ist die Gleichung derjenigen Kurve gesucht, auf der alle relativen Hochpunkte der Schar liegen.)
Lösung (nach der 1. Methode)
1. Schritt:x- und y-Koordinate des relativen Hochpunkts berechnen
Damit wir die Funktionenschar besser ableiten können, quadrieren wir die Klammer mit Hilfe der zweiten binomischen Formelund multiplizieren anschließend das vor der Klammer stehende x in die Klammer hinein. Den Bruch 
lassen wir außerhalb der Klammer stehen. (Rein theoretisch könntest du den Bruch auch in die Klammer hineinmultiplizieren, doch dadurch ergeben sich nur viele unangenehme Brüche und das macht dir das Ableiten bestimmt nicht leichter.) Wenn man 
ableitet, bleibt der Bruch nämlich einfach stehen, da es sich um eine multiplikative Konstante handelt. Deshalb ist es besser den Bruch nicht mit der Klammer zu multiplizieren. Das vor der Klammer stehende x musst du aber in die Klammer hinein multiplizieren. Wenn du es nicht machen würdest, bräuchtest du nämlich zum Ableiten Die Produktregel, was viel umständlicher wäre.
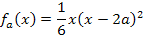
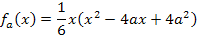
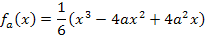
In dieser Form lässt sich die Ableitung leicht bilden. Achte aber darauf, dass du nach x ableiten musst und nicht etwa nach a. Du musst dich also beim Ableiten besonders auf die Potenzen von x konzentrieren. (Nur die ursprünglichen Potenzen von x jeweils nach vorne ziehen und diese Potenzen um 1 verringern, nicht die Potenzen von a!)
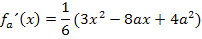
Um die x-Koordinaten der relativen Hochpunkte der Schar zu berechnen, muss die erste Ableitung gleich Null gesetzt werden.
