Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
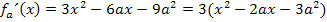
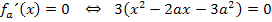
Dividiert man diese Gleichung durch 3, erhält man:
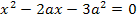
Diese Gleichung lösen wir mit der Mitternachtsformel nach x auf:
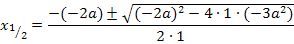
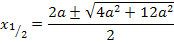
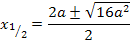
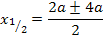
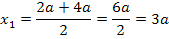
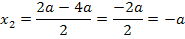
Jetzt müssen wir herausfinden, welche der beiden berechneten x-Koordinaten zum relativen Tiefpunkt der Schar gehört. Wir verwenden hier die Zweite Ableitung f´´(x), um das herauszufinden. (Stattdessen kannst du auch die Monotonie von 
untersuchen, das ist aber umständlicher.) Wir ermitteln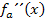 
und setzen nacheinander die ermittelten x-Koordinaten in 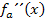ein. Wo ein Tiefpunkt vorliegt, muss der Graph linksgekrümmt sein, d.h. es muss bei der zweiten Ableitung etwas Positives herauskommen. Wenn dabei etwas Negatives herauskommt, liegt sicher ein Hochpunkt vor. (Ist das Ergebnis gleich Null, ist keine Aussage möglich.)
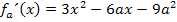
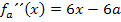
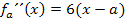
x-Koordinaten einsetzen in die zweite Ableitung:
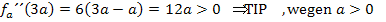
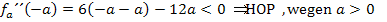
Laut Angabe gilt a >0 und somit auch 12a >0. Bei x = 3a ist die zweite Ableitung deshalb positiv und es liegt an dieser Stelle ein relativer Tiefpunkt der Schar vor. Daher wissen wir nun, dass der Tiefpunkt die x-Koordinate x = 3a besitzt. (Vorsicht:Wenn a negativ gewesen wäre, hätte an der Stelle x = 3a ein relativer Hochpunkt der Schar vorgelegen!)
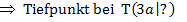
Anmerkung:Manchmal kann es auch vorkommen, dass die berechnete x-Koordinate des entsprechenden Punktes von a unabhängig ist, d.h. es kommt dabei kein a mehr vor. Wenn das der Fall ist, bist du schon fertig und musst nicht mehr weiterrechnen, denn das Ergebnis der x-Koordinate ist dann schon die gesuchte Gleichung der Ortskurve. Wenn man beispielsweise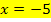 
, also den Tiefpunkt 
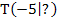erhalten hätte, würde die Gleichung der Ortskurve der TIP einfach 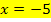lauten. Durch die Gleichung 
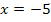ist eine senkrechte Gerade beschrieben, welche die x-Achse bei -5 schneidet. Auf dieser Geraden liegen dann alle TIP der Schar.
In unserem Beispiel liegt der Tiefpunkt bei T(3a|?). Die x-Koordinate des TIP ist also x = 3a ;sie ist offensichtlich noch abhängig von a;es kommt schließlich ein a in der x-Koordinate vor. Wir müssen deshalb noch weiterrechnen, um die Ortskurve der TIP zu ermitteln.
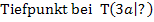
2. Schritt:Fasse die ermittelte x-Koordinate als Gleichung auf. Stelle diese Gleichung nach dem Parameter a um und setze das Ergebnis für a in die Funktionsgleichung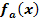 
ein. Dies liefert die Gleichung der Ortskurve der TIP.
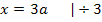
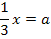
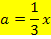
Einsetzen von a in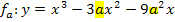 
ergibt:
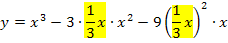
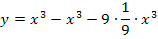
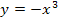
Dies ist die gesuchte Ortskurve der TIP. Das bedeutet, dass alle Tiefpunkte der Schar
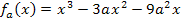mit a >0 auf der Funktion 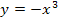liegen.
