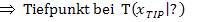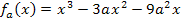Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Enthält eine der beiden Koordinaten den Parameter nicht, liefert diese Koordinate direkt die Gleichung der gesuchten Ortskurve.
Enthält keine der beiden Koordinaten den Parameter, ist der jeweilige Punkt unabhängig vom Scharparameter. (Es kommt dann also weder in der x-Koordinate noch in der y-Koordinate der Parameter vor;beide Koordinaten sind richtige Zahlen ohne Parameter.) Das bedeutet, dass dieser eine Punkt gemeinsamer HOP oder TIP bzw. WEP aller Graphen der Schar ist. Dann gibt es bei dieser speziellen Schar keine Ortskurve für diesen Punkt. Alle Graphen der Schar haben dann den gleichen HOP, TIP bzw. WEP, je nach dem, um was für einen Punkt es eben geht. In so einem Fall wird aber bestimmt nicht nach einer Ortskurve für diese Art von Punkt gefragt sein;es gibt dann schließlich gar keine solche Ortskurve!
Man würde als Lehrer dann vermutlich eher die folgende Aufgabenstellung wählen:„Zeige, dass alle Graphen der Schar einen gemeinsamen HOP (oder TIP bzw. WEP) haben und gib seine Koordinaten an!“ Bei so einer Aufgabe musst du den jeweiligen Punkt ausrechnen und zeigen, dass er unabhängig vom Scharparameter gilt. Dies kann nur dann der Fall sein, wenn der Scharparameter bei keiner der Koordinaten vorkommt. Es müssen sich also jeweils richtige Zahlen (ohne a) für x- und y-Koordinate des Punktes ergeben. Außerdem muss für jedes a die hinreichende Bedingung für diese Art von Punkt erfüllt sein. D.h. zum Beispiel, dass bei einem Hochpunkt für jedes a die zweite Ableitung an der entsprechenden Stelle negativ sein muss, oder bei einem Wendepunkt die dritte Ableitung an dieser Stelle für jedes a ungleich Null sein muss. (Falls dir jetzt noch nicht ganz klar sein sollte, wie man das zeigt, keine Sorge! Es folgt nachher noch ein gesondertes Aufgabenbeispiel dazu. Siehe 7. Bsp.!)
Anleitung zur Berechnung einer Ortskurve 2. Methode (am Beispiel der Ortskurve der relativen Tiefpunkte)
Wir betrachten jetzt die Schar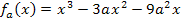 
mit a >0.
Gesucht ist die Kurve, auf der alle relativen Tiefpunkte der Schar liegen, also die Ortskurve der relativen Tiefpunkte der Schar 
1. Schritt:Berechnung der x- Koordinate der relativen Tiefpunkte von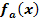 
in Abhängigkeit von a
D.h. es darf bei der Berechnung der TIP für a keine konkrete Zahl eingesetzt werden, man muss sich allerdings denken, dass a eine richtige Zahl sei. Man muss also mit a rechnen, als wenn a eine normale Zahl wäre. Im Ergebnis der x- Koordinate kommt der Parameter a in der Regel noch vor.
