Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Wenn entweder bei der x-Koordinate oder bei der y-Koordinate des HOP kein a enthalten ist, musst du gar nichts mehr rechnen! Die jeweilige Koordinate ohne a entspricht dann nämlich schon der Gleichung der gesuchten Ortskurve.
Wenn man beispielsweise den Hochpunkt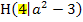 
erhalten hätte, würde die Gleichung der Ortskurve der HOP einfach 
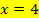lauten. Durch die Gleichung 
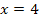ist eine senkrechte Gerade beschrieben, welche die x-Achse bei 4 schneidet. Auf dieser Geraden liegen dann alle HOP der Schar. Weil die Hochpunkte 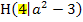alle die gleiche x-Koordinate x = 4 haben und sich nur in ihrer y-Koordinate unterscheiden, müssen sie senkrecht übereinander auf der Geraden x = 4 liegen.
Hätte sich dagegen zum Beispiel der Hochpunkt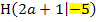 
ergeben, würde die Gleichung der Ortskurve 
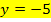lauten. Durch die Gleichung 
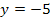ist eine waagrechte Gerade beschrieben, welche die y-Achse bei -5 schneidet. Auf dieser Geraden liegen dann alle HOP der Schar. Alle Hochpunkte der Schar haben schließlich die y-Koordinate 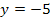, aber sie unterscheiden sich in ihrer x-Koordinate, weil die x-Koordinate schließlich noch von a abhängt. (Bei der x-Koordinate kommt ja ein a vor.) Für verschiedene Werte von a ergeben sich also unterschiedliche x-Koordinaten, aber die y-Koordinate bleibt immer 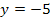. (Bei der y-Koordinate kommt ja kein a vor.) Man sagt, die y-Koordinate ist unabhängig vom Scharparameter a. Daher müssen alle Hochpunkte 
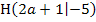auf der waagrechten Geraden 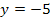liegen. 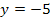ist dann die Gleichung der Ortskurve der HOP.
Bei der Ermittlung einer Ortskurve der Tiefpunkte bzw. Wendepunkte einer gegebenen Schar geht man entsprechend vor wie bei der Ortskurve der Hochpunkte, bloßdass man natürlich mit den Koordinaten der Tief- bzw. Wendepunkte arbeitet.
Um die Gleichung der Ortskurve der TIP zu berechnen, ermittelst du vorweg die x- und y-Koordinate des TIP der gegebenen Schar. Wenn sowohl die x- als auch die y-Koordinate den Parameter enthält, löst du wieder Gleichung I., die sich aus der x-Koordinate des TIP ergeben hat, nach dem Parameter auf und setzt das Ergebnis in die Gleichung II ein, welche sich aus der y-Koordinate des TIP ergeben hat. So erhältst du die Gleichung der Ortskurve der TIP einer bestimmten Schar.
Ist die Gleichung der Ortskurve der WEP einer bestimmten Schar gesucht, berechnest du logischerweise zuerst die Koordinaten des WEP. Dann wieder entsprechend vorgehen wie oben schon bei der Berechnung der Ortskurve der HOP bzw. TIP erklärt.
| Zusammenfassung: Ortskurve ermitteln (1. Methode)
Die Vorgehensweise bei der Berechnung einer Ortskurve der TIP, einer Ortskurve der HOP oder einer Ortskurve der WEP ist vom Prinzip jeweils gleich. · Jeweiligen Punkt (HOP, TIP oder WEP) in Abhängigkeit vom Parameter berechnen, also seine x- und y-Koordinate ausrechnen ohne für den Parameter etwas Konkretes einzusetzen. Das ergibt die Gleichungen I. und II., wobei Gleichung I. aus der x-Koordinate und Gleichung II. aus der y-Koordinate des jeweiligen Punktes folgt. · Parameter aus den Gleichungen eliminieren, indem du Gleichung I. nach dem Parameter auflöst und in II. einsetzt. Das Eliminieren des Parameters ist natürlich nur dann nötig, wenn der Parameter in beiden Koordinaten auftritt. · Definitionsmenge der Ortskurve angeben |
azu musst du dir überlegen, welche Werte die jeweilige x-Koordinate des HOP, TIP bzw. WEP überhaupt annehmen kann. Dies hängt unter anderem von den Werten des Parameters ab, die in der jeweiligen Aufgabe zugelassen sind. Du musst also ganz genau lesen, welche a bei der Funktionenschar zugelassen sind, also ob da steht a 
ℝ oder vielleicht nur a >0 oder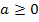 
. (Näheres dazu gleich bei der Anleitung zur 2. Methode.)
