Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Zum Beispiel könnte dabei folgendes herausgekommen sein:
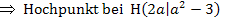
(Dieser Punkt hat nichts mit der oben genannten Schar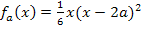 
und der oben gezeigten Abbildung zu tun. Es handelt sich bei dem Hochpunkt 
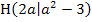nur um ein willkürlich gewähltes Beispiel, woran die weitere Vorgehensweise erklärt werden soll. 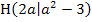ist also nicht der Hochpunkt der oben erwähnten Schar 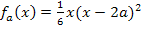. Die Ortskurve der Schar 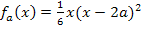sollst du nämlich anschließend selbst ausrechnen. Die zugehörige Rechnung folgt weiter unten.)
2. Schritt:Parameter eliminieren (Das bedeutet so viel wie „a herauswerfen“, weil in diesem Beispiel der Parameter mit a bezeichnet ist. Wenn der Parameter k oder t heißt, muss man natürlich k bzw. t herauswerfen.)
Wir bleiben bei dem Beispiel Hochpunkt 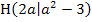. Es sind jetzt also die x- und y-Koordinate des Hochpunktes H in Abhängigkeit von a bekannt. Wir fassen nun jede Koordinate des Hochpunktes als einzelne Gleichung auf. In unserem Beispiel gilt:
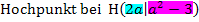
Gleichung I. kommt von der x-Koordinate des Hochpunktes;Gleichung II. kommt von der y-Koordinate des Hochpunktes. Es liegen uns jetzt zwei Gleichungen I. und II. vor, die beide den Parameter a enthalten. (Das ist bei den meisten Aufgaben so, in denen nach einer Ortskurve gefragt ist. Nur selten ist bei einer oder bei beiden der Gleichungen kein Parameter mehr enthalten. Wie man dann vorgeht, besprechen wir gleich noch. Siehe unten!)
Weitere Vorgehensweise, wenn in beiden Koordinaten / in beiden Gleichungen der Parameter a vorkommt:
Gleichung I. nach a auflösen und das Ergebnis in Gleichung II. für jedes dort vorkommende a einsetzen
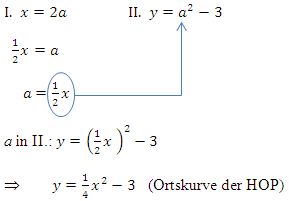
Durch das Auflösen von I. nach a und anschließendem Einsetzen in II. ist der Parameter a vollständig weggefallen. Mathematisch gesagt, a wurde eliminiert. Die dadurch entstehende Gleichung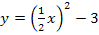 
ist an sich bereits die gesuchte Ortskurve der HOP. Sie muss allerdings noch vereinfacht werden. So kommt man dann auf 
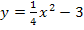, also auf die Gleichung der gesuchten Ortskurve der Hochpunkte. Die Gleichung 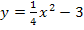beschreibt eine nach oben geöffnete Parabel, die breiter ist als die Normalparabel. Die Hochpunkte 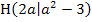liegen alle auf dieser Parabel.
Nun fragst du dich wahrscheinlich, was man denn macht, wenn entweder bei der x-Koordinate des HOP oder bei der y-Koordinate des HOP überhaupt kein a vorkommt. Dann kann man schließlich Gleichung I. nicht nach a auflösen und in II. einsetzen.
Weitere Vorgehensweise, wenn in einer der beiden Koordinaten / in einer der beiden Gleichungen der Parameter a nicht vorkommt:
