Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
h. gesucht ist die Ortskurve der Wendepunkte.)
Lösung:
Gegeben ist also die Schar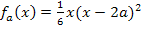 
mit a >0. Damit du dir die Schar besser vorstellen kannst, sind die Graphen für a = 1, a = 2 , a = 3 und a = 4 in der folgenden Abbildung dargestellt. Der Graph 
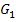, d.h. der zu a = 1 gehörende Graph, ist in Graublau gezeichnet. Der zu a = 2 gehörende Graph 
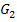ist in Hellgrau gezeichnet, der Graph 
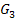zu a = 3 in Dunkelgrau und der Graph 
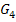zu a = 4 in Lila.
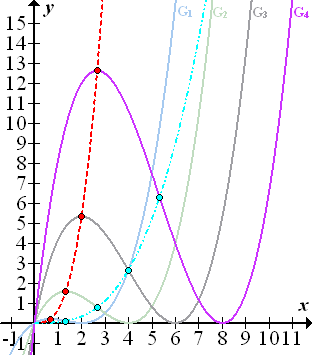
Abb.:Die Graphen der Schar 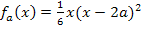für a = 1, a = 2 , a = 3 und a = 4 zusammen mit der Ortskurve der relativen Hochpunkte 
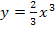(rot gestrichelt) und der Ortskurve der Wendepunkte 
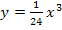(hellblau gestrichpunkted)
Betrachte nun in der Abbildung ausschließlich die rot markierten Hochpunkte der verschiedenen Funktionen der Schar. Du siehst, dass sie alle auf der rot gestrichelten Kurve liegen. Diese rot gestrichelte Kurve ist die Ortskurve der Hochpunkte dieser Schar. Sie hat die Gleichung 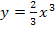. Wie man auf diese Gleichung kommt, wird weiter unten noch erklärt. Aber vorher noch zur Ortskurve der Wendepunkte in diesem Beispiel. In der Abbildung sind die Wendepunkte der einzelnen Funktionen der Schar hellblau markiert. Wie du leicht erkennen kannst, liegen alle Wendepunkte dieser Schar auf der hellblau gestrichpunkteten Kurve. Diese Kurve ist die Ortskurve der Wendepunkte von 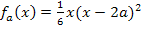. Die Ortskurve der Wendepunkte hat in diesem Beispiel die Gleichung 
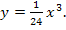(Die zugehörige Rechnung folgt weiter unten.)
Es ist zwar in der Aufgabe nicht danach gefragt, aber was ist hier mit der Ortskurve der Tiefpunkte? Die Tiefpunkte liegen bei dieser Schar offensichtlich alle auf der x-Achse. Alle Tiefpunkte der Schar haben demnach die y-Koordinate y = 0, die einzelnen Tiefpunkte unterscheiden sich nur in ihrer x-Koordinate. Daher ist die x-Achse hier die Ortskurve der Tiefpunkte;sie hat bekanntlich die Gleichung y = 0.
Hinweis:Statt Ortskurve kann man übrigens auch Ortslinie oder geometrischer Ort sagen. Ortskurve, Ortslinie oder geometrischer Ort sind gleichbedeutende Formulierungen. Es macht also keinen Unterschied, ob nach der Ortskurve, nach der Ortslinie oder nach dem geometrischen Ort beispielsweise der relativen Hochpunkte einer bestimmten Schar gefragt ist. Genauso gut hätte auch nach der Gleichung derjenigen Kurve gefragt sein können, auf der alle relativen Hochpunkte der Schar liegen. Das sind alles bloßunterschiedliche Formulierungen der gleichen Aufgabe.
