Prinzip dieses Beweise
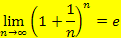
Um zu beweisen, dass die Folge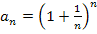 
für 
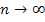tatsächlich einen Grenzwert besitzt, welchen wir als die Zahl e definieren, geht man folgendermaßen vor:Man konstruiert eine Intervallschachtelung mit Hilfe zweier Folgen 
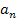und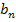 
, die beide den Grenzwert e haben. Die Folge 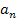soll mit wachsendem n streng monoton zunehmen, die andere Folge 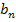streng monoton abnehmen. Die Folge 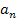nähert sich von unten an den gesuchten Grenzwert e an und die Folge 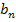von oben. Die Zahl e wird somit von diesen beiden Zahlenfolgen quasi in die Zange genommen.
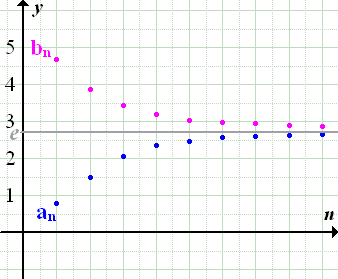
Die Folge 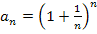ist die gegebene Folge;sie hat den Grenzwert e und ist streng monoton steigend. Dies muss man natürlich noch beweisen. Sie nähert sich quasi von unten an e an. Als zweite Folge 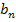verwendet man am besten: 
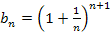Diese Folge hat auch den Grenzwert e und ist streng monoton fallend, was natürlich ebenfalls zu beweisen ist. Sie nähert sich von oben an e an. Da die Folgen 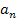und 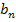den gleichen Grenzwert besitzen, muss die Differenz beider Folgen 
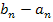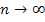für gegen Null gehen. Man sagt:„ 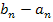ist eine Nullfolge.“ (Eine Nullfolge hat für 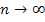immer den Grenzwert Null.) Wenn wir das beweisen können, muss der Grenzwert 
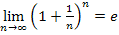existieren.
Es muss demnach gezeigt werden:
1. Die Folge 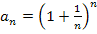ist streng monoton steigend.
2. Die Folge 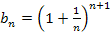ist streng monoton fallend.
3. Die Differenzfolge 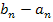geht für 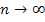gegen Null.
Zu 1. Die Folge 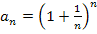ist streng monoton steigend genau dann, wenn gilt:
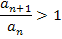
Erklärung:Wenn 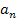ein bestimmtes Glied der Folge ist, ist 
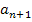das nachfolgende Glied dieser Folge. Wenn eine Folge streng monoton steigend ist, muss das nachfolgende Glied 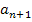größer als das Glied 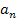selbst sein. Ein Bruch ist immer dann größer als 1, wenn der Zähler größer ist als der Nenner. Daher muss der Bruch 
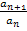größer als 1 sein, wenn die Folge 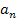streng monoton steigend ist. Umgekehrt kann auch von 
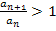darauf geschlossen werden, dass die Folge 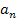streng monoton steigend ist.
Zu 2. Die Folge 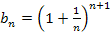ist streng monoton fallend genau dann, wenn gilt:
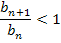
Erklärung:Wenn 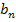ein bestimmtes Glied der Folge ist, ist 
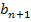das nachfolgende Glied dieser Folge. Wenn eine Folge streng monoton fallend ist, muss das nachfolgende Glied 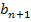kleiner als das Glied 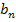selbst sein. Ein Bruch ist immer dann kleiner als 1, wenn der Zähler kleiner ist als der Nenner. Daher muss der Bruch 
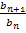kleiner als 1 sein, wenn die Folge 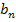streng monoton fallend ist. Umgekehrt kann auch von 
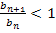darauf geschlossen werden, dass die Folge 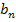streng monoton fallend ist.
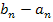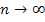Zu 3. Wenn die Differenzfolge für gegen Null geht, müssen die Folgen 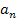und 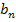beide den gleichen Grenzwert besitzen. Wir bezeichnen diesen Grenzwert als Eulersche Zahl e. So lässt sich die Existenz des Grenzwertes 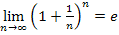für n 
ℕ beweisen.
Auch die Existenz des Grenzwertes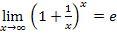 
für beliebige reelle Zahlen x kann gezeigt werden. Auf die genaue Beweisführung soll hier verzichtet werden.
