Grenzwerte von e- und ln-Funktionen
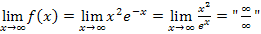
Nun kann die Regel von L´Hospital angewendet werden:Zähler ableiten und Nenner ableiten, dann erneut versuchen den Grenzwert zu ermitteln.
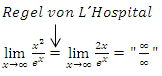
Leider hat sich auch nach der erstmaligen Anwendung der Regel von L´Hospital wieder ein unbestimmter Ausdruck ergeben. Wir müssen die Regel von L´Hospital ein zweites Mal anwenden:Noch einmal Zähler und Nenner getrennt ableiten, dann wiederum versuchen den Grenzwert zu ermitteln.
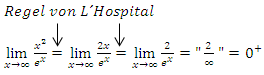
Nach zweimaliger Anwendung der Regel von L´Hospital lässt sich der Grenzwert endlich berechnen. Wir erhalten logischerweise das gleiche Ergebnis, wie schon bei den anderen beiden Methoden.
Merke:Man darf die Regel von L´Hospital so oft hintereinander anwenden bis sich kein unbestimmter Ausdruck mehr ergibt und man den Grenzwert ausrechnen kann.
Beispiel für die dreimalige Anwendung der Regel von L´Hospital:
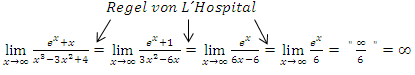
Wir haben nun alle möglichen Methoden besprochen, wie man Grenzwerte ermitteln kann, die zu unbestimmten Ausdrücken führen. Du musst selbst natürlich nur eine der drei Methoden sicher beherrschen. Versuche dich doch gleich mal an der nächsten Beispielaufgabe. Einer der dabei gesuchten Grenzwerte, führt ebenfalls zu einem unbestimmten Ausdruck.
3. Bsp.:
Untersuche das Verhalten der Funktion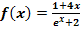 
an den Rändern des Definitionsbereichs!
Lösung:
Um das Verhalten der Funktion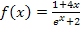 
an den Rändern ihres Definitionsbereichs untersuchen zu können, muss vorweg der maximale Definitionsbereich von 
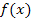bestimmt werden. Das geht ganz leicht. Wir wissen, dass die e-Funktion für beliebige reelle Zahlen definiert ist. Bei 
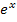kann man also alles einsetzen;dabei gibt es kein Problem. Der Nenner des Bruchs darf außerdem nicht Null ergeben. Da 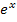immer positiv ist, ist aber auch der Nenner 
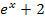immer positiv. (Zählt man zu einer positiven Zahl etwas dazu, ist das Ergebnis ebenfalls ganz bestimmt wieder positiv, da das Ergebnis ja noch größer ist als die ursprüngliche, bereits positive Zahl.) Der Nenner 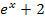kann demnach gar nicht gleich Null werden, egal was für x eingesetzt wird. Die Funktion 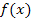ist also für sämtliche reellen Zahlen definiert.
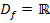
Die Ränder des Definitionsbereichs liegen deshalb bei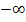 
und 
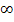. Wir müssen also die folgenden Grenzwerte ermitteln:
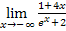und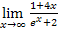 
Wir beginnen mit dem Verhalten für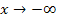 
;das ist der einfachere der beiden gesuchten Grenzwerte.
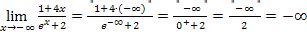
Nun zum Verhalten für 
;das wird etwas schwieriger.
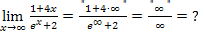
ist ein unbestimmter Ausdruck. Um zu ermitteln, was dabei herauskommt, stehen uns die oben schon ausführlich besprochenen drei Wege zur Verfügung.
