Grenzwerte von e- und ln-Funktionen

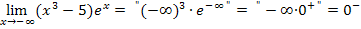
Kommt dagegen das Unendlich von einer e-Funktion und die Null zum Beispiel von einer gebrochenrationalen Funktion, so überwiegt das von der e-Funktion kommende Unendlich und es gilt: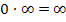

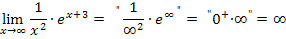
Es setzt sich immer das durch, was von der e-Funktion kommt. Umgekehrt kommt bei einem Grenzwert der Form 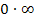mit ln immer das heraus, was nicht vom ln kommt, sondern vom anderen Faktor. (Das Vorzeichen des Ergebnisses muss man sich allerdings noch gesondert überlegen;es gelten die allgemeinen Vorzeichenregeln der Multiplikation bzw. Division.)

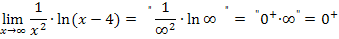
Schüler eines bayerischen Gymnasiums G8 dürfen sich in der Regel Grenzwerte, die zu einem unbestimmten Ausdruck führen, nach der beschriebenen Art überlegen. G 8 –Schüler dürfen z. B. mit der Begründung „e-Funktion wächst stärker“ das jeweilige Ergebnis des Grenzwertes einfach hinschreiben. Allerdings reicht das nicht allen Lehrern. Manche verlangen zusätzlich eine Rechnung. Entweder man verwendet zur Berechnung unbestimmter Ausdrücke die Regeln von L´Hospital (falls im Unterricht besprochen) oder man formt die Funktion, deren Grenzwert berechnet werden soll, so um, dass man auf bekannte Grenzwerte (vergleiche Formelsammlung bzw. Merkhilfe) zurückgreifen kann. Das hängt davon ab, wie es im Unterricht vorgeführt wurde. Schau einfach in dein Mathe-Schulheft und suche nach einer Aufgabe mit einem unbestimmten Ausdruck, die dein(e) Lehrer(in) gerechnet hat. So wie es dein(e) Lehrer(in) gemacht hat, machst du es ebenfalls. Im Folgenden werden an einem konkreten Beispiel alle drei Lösungswege gezeigt, damit du dir den für dich passenden Rechen- bzw. Lösungsweg heraussuchen kannst.

2. Bsp.:

Gegeben ist die Funktion .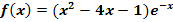

Es soll das Verhalten für 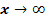untersucht werden.

Lösung:

Gesucht ist hier der folgende Grenzwert: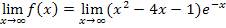

Es ist hier also der Grenzwert eines Produkts zu ermitteln. Daher überlegt man sich zuerst, wogegen die einzelnen Faktoren des Produkts gehen.

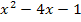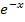Der erste Faktor, also das Polynom , geht für gegen Unendlich. (Wie man darauf kommt, wird gleich noch näher erläutert.) Der zweite Faktor, also , geht für gegen 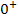. Bei der Berechnung des Grenzwertes ergibt sich also der unbestimmte Ausdruck 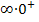. Wir können das Ergebnis auf die drei folgenden Arten herausfinden.

1. Methode:Nur mit Überlegung, ohne konkrete Rechnung

Notwendige Vorüberlegungen:

Bei der Funktion 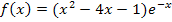ist der erste Faktor 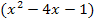ein Polynom. Um herauszufinden, was bei 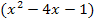für herauskommt, genügt es nur die höchste x-Potenz 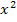zu betrachten. D.h. du kannst die niedrigeren Potenzen des Polynoms komplett außer Acht lassen. Das x mit der höchsten Potenz setzt sich gegenüber den niedrigeren Potenzen durch, weil es stärker wächst als die anderen. Du setzt also das Unendlich in Gedanken nur bei 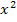ein, nicht aber bei 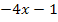. Weil 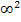wieder 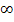ergibt, geht 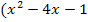) für gegen Unendlich.

---