Grenzwerte von e- und ln-Funktionen

Bei ist beispielsweise zu beurteilen, ob der Zähler oder der Nenner schneller gegen Unendlich strebt. Man muss sich also überlegen, ob der Zähler oder der Nenner schneller wächst:

Wächst der Zähler stärker als der Nenner, so gilt: 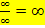(Sehr große Zahl durch kleinere Zahl wird sehr groß, also unendlich. Vorzeichen extra überlegen!)

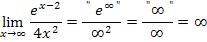
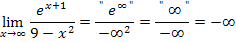
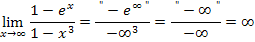
Bei den soeben gezeigten drei Beispielen kommt das Unendlich im Zähler jeweils von einer e-Funktion, wogegen das Unendlich im Nenner von einer Polynomfunktion kommt. Eine e-Funktion wächst schneller als jedes Polynom. Daher setzt sich das Unendlich des Zählers quasi gegenüber dem Unendlich des Nenners durch. Der Zähler wächst jeweils schneller als der Nenner und es ergibt sich deswegen insgesamt Unendlich bzw. Minus-Unendlich.

Das Vorzeichen des Ergebnisses wird jeweils nach den Vorzeichenregeln der Division bestimmt: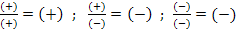

Beim nächsten Beispiel wächst ebenfalls der Zähler schneller als der Nenner, weil in diesem Fall das Unendlich im Zähler von einer Polynomfunktion kommt und das Unendlich im Nenner von einer ln-Funktion. Die ln-Funktion wächst bekanntlich langsamer als jedes Polynom. Daher setzt sich auch hierbei das Unendlich des Zählers quasi gegenüber dem Unendlich des Nenners durch.

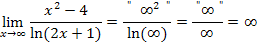
Wächst der Nenner stärker als der Zähler, so gilt: 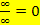(Kleinere Zahl durch sehr große Zahl wird sehr klein, also fast Null. Vorzeichen extra überlegen!)

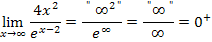
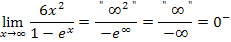
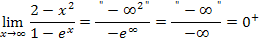
Bei diesen drei Beispielen kommt das Unendlich im Nenner jeweils von einer e-Funktion, wogegen das Unendlich im Zähler von einer Polynomfunktion kommt. Die e-Funktion wächst schneller als die Polynomfunktion;also überwiegt quasi das Unendlich im Nenner und es kommt insgesamt Null heraus. Das Gleiche gilt für das nächste Beispiel, da hier das Unendlich im Nenner von einer Polynomfunktion kommt, welches stärker ist als das Unendlich im Zähler, das von einer ln-Funktion kommt.

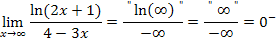
Sind Zähler und Nenner jeweils gleich stark, weil sie zum Beispiel beide eine e-Funktion enthalten, dann hilft es in der Regel, wenn man jeweils die höchste Potenz mit x im Zähler und Nenner ausklammert und danach weg kürzt. Danach lässt sich der Grenzwert eindeutig berechnen. Es ergibt sich dann nämlich kein unbestimmter Ausdruck mehr. Das Ergebnis des Grenzwertes ist in diesem Fall eine konkrete reelle Zahl.

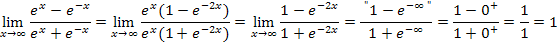
Bei 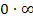ist zu überlegen, ob sich die Null gegenüber dem Unendlich durchsetzt oder entsprechend umgekehrt.

Kommt die Null von einer e-Funktion und das Unendlich von einer Polynomfunktion oder einer ln-Funktion, so überwiegt die von der e-Funktion kommende Null und es gilt:

---