Grenzwerte von e- und ln-Funktionen
Achtung:Du darfst nicht einfach davon ausgehen, dass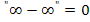 
stimmt. Das kann stimmen, muss aber nicht! Es kann genauso gut Unendlich oder Minus-Unendlich dabei herauskommen. Es hängt nämlich davon ab, welches Unendlich stärker ist, oder genauer gesagt, welche Teilfunktion schneller wächst und somit schneller gegen Unendlich geht. Wenn du auf 
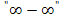stößt, solltest du bei der gegebenen Funktion vorher so ausklammern, dass sich nachher nicht mehr 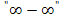ergibt, sondern ein Produkt, von dem sich der Grenzwert dann besser berechnen lässt.
Das klappt zum Beispiel bei dem Grenzwert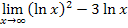 
.
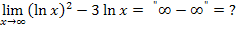
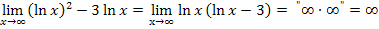
Bei Grenzwerten mit Logarithmus hilft es manchmal auch, vorweg bei der gegebenen Funktion eines der Logarithmus-Rechengesetze anzuwenden. (Siehe auch: 2a. Gleichungen mit lnx oder 
lösen, einschließlich ln-Rechengesetze)
So kann man zum Beispiel den Grenzwert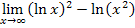 
berechnen.
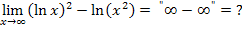
Laut dem ln-Rechengesetz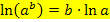 
gilt für x >0 auch: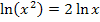 
Die Funktion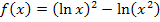 
ist sowieso nur für x >0 definiert. Daher dürfen wir die Umformung 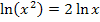ohne Einschränkung durchführen.
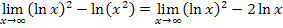
Nun lässt sich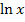 
bequem ausklammern und der gesuchte Grenzwert berechnen.
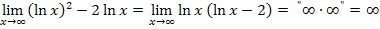
Ein ähnliches Problem wie bei 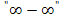tritt auch bei 
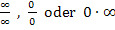auf. Auch bei diesen Ausdrücken kann man allgemein nicht sagen, was herauskommt;das hängt vom jeweiligen Einzelfall ab. Es handelt sich dabei um „unbestimmte Ausdrücke“.
Wenn man den Grenzwert einer komplizierteren e- oder ln-Funktion berechnen muss, passiert es oft, dass man auf einen sogenannten „unbestimmten Ausdruck“ stößt.
Zu den unbestimmten Ausdrücken zählen insbesondere die Ausdrücke der folgenden Form: 
(Von den Vorzeichen wurde hier abgesehen. Statt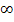 
kann auch 
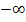vorkommen.)
Bei unbestimmten Ausdrücken kann man nicht generell sagen, was heraus kommt! Das Ergebnis so eines Ausdrucks kann Null, Unendlich bzw. Minus-Unendlich oder eine konkrete Zahl sein.
Das Ergebnis kann nur im jeweiligen Einzelfall ermittelt werden. Es hängt bei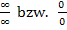 
davon ab, welches 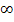bzw. welche 0 sich durchsetzt, also von welcher Funktion das jeweilige 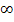bzw. die Null kommt. Bei 
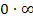ist zu überlegen, ob sich die Null gegenüber dem Unendlich durchsetzt oder entsprechend umgekehrt das Unendlich gegenüber der Null. Aber wie geht das?
Wir wissen:
Die e-Funktion wächst schneller als jedes Polynom oder eine ln-Funktion.
Die ln-Funktion wächst dagegen langsamer als jedes Polynom und die e-Funktion.
Daraus folgt die Faustregel:Die e-Funktion überwiegt, die ln-Funktion unterliegt!
In anderen Worten:
Ein Unendlich, das von einer e-Funktion kommt, ist stärker als ein Unendlich von einer Polynomfunktion oder einer ln-Funktion. Ebenso überwiegt eine Null, die von einer e-Funktion kommt, immer im Vergleich zu einer Null, die von einer Polynomfunktion kommt. Umgekehrt unterliegt das Unendlich, welches von einer ln-Funktion kommt, im Vergleich zu einem Unendlich, das von einer Polynomfunktion oder einer e-Funktion kommt.
