Grenzwerte von e- und ln-Funktionen
Du denkst dir quasi folgendes:
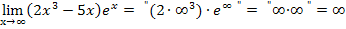
Wie oben schon erwähnt solltest du das in Prüfungen so nicht hinschreiben. Die beiden Zwischenschritte, die in Anführungszeichen gesetzt sind, bitte weglassen!
Eine mathematisch korrekte Schreibweise ist beispielsweise:
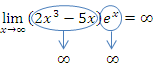
So oder ähnlich kannst du das also auch in Prüfungen schreiben.
Für  geht die Funktion
geht die Funktion 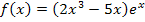 gegen
gegen 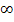 . Die Funktionswerte von
. Die Funktionswerte von 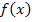 nehmen für
nehmen für  , also ganz weit rechts im Koordinatensystem, unendlich große Werte an. Anschaulich bedeutet das, dass der Graph der Funktion
, also ganz weit rechts im Koordinatensystem, unendlich große Werte an. Anschaulich bedeutet das, dass der Graph der Funktion 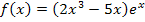 im Koordinatensystem nach rechts oben geht.
im Koordinatensystem nach rechts oben geht.
Zu 1b.)
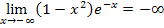
Wie kommt man auf dieses Ergebnis? Ganz einfach, man geht im Prinzip wie in Teilaufgabe 1a.) vor. Man überlegt sich also zuerst einzeln, wohin die Faktoren 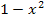 und
und 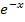 für
für 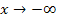 gehen. Dazu setzt du in Gedanken
gehen. Dazu setzt du in Gedanken 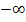 für x ein.
für x ein.
Der Faktor 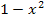 geht für
geht für 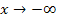 offensichtlich gegen
offensichtlich gegen 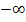 :
:
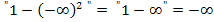
Der Faktor 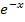 geht für
geht für 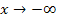 gegen
gegen 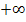 :
:
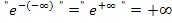
Insgesamt ergibt sich dann:
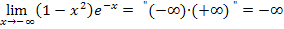
Den Zwischenschritt mit den Anführungszeichen bitte bei Prüfungen nicht hinschreiben! Besser eine der beiden folgenden Schreibweisen wählen:
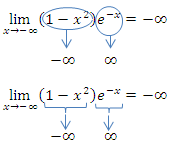
Für 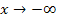 geht die Funktion
geht die Funktion 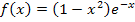 gegen
gegen 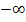 . Die Funktionswerte von
. Die Funktionswerte von 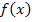 nehmen für
nehmen für 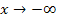 , also ganz weit links im Koordinatensystem, unendlich kleine Werte an. Was bedeutet dieses Ergebnis anschaulich? Der Graph der Funktion
, also ganz weit links im Koordinatensystem, unendlich kleine Werte an. Was bedeutet dieses Ergebnis anschaulich? Der Graph der Funktion 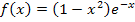 läuft im Koordinatensystem nach links unten.
läuft im Koordinatensystem nach links unten.
Zu 1c.)
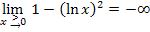
Erläuterung:
Hier ist der rechtsseitige Grenzwert der Funktion 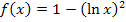 an der Stelle x = 0 gesucht. (Das erkennt man an dem Größer-Zeichen bei
an der Stelle x = 0 gesucht. (Das erkennt man an dem Größer-Zeichen bei 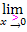 .) In anderen Worten:Wir sollen uns von rechts, also vom Positiven, an die Stelle x = 0 annähern, d.h.
.) In anderen Worten:Wir sollen uns von rechts, also vom Positiven, an die Stelle x = 0 annähern, d.h. 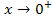 . Die ln-Funktion
. Die ln-Funktion 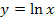 ist bekanntlich nur für positive Zahlen definiert;an der Stelle x = 0 ist sie also nicht definiert, deshalb müssen wir ja den Grenzwert
ist bekanntlich nur für positive Zahlen definiert;an der Stelle x = 0 ist sie also nicht definiert, deshalb müssen wir ja den Grenzwert 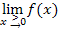 berechnen und nicht einfach
berechnen und nicht einfach 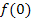 .
.
Wir machen uns vorweg bewusst, wie sich die ln-Funktion 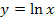 für
für 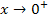 verhält. Ihr Graph hat die y-Achse als senkrechte Asymptote, er kommt von rechts an die y-Achse heran und schießt dort steil nach unten.
verhält. Ihr Graph hat die y-Achse als senkrechte Asymptote, er kommt von rechts an die y-Achse heran und schießt dort steil nach unten.
Deswegen gilt: 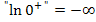
Daraus folgt:
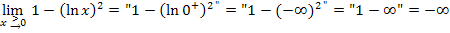
Was bedeutet dieses Ergebnis anschaulich für den Graph der Funktion 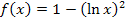 ? Ihr Graph nähert sich von rechts an die y-Achse an und schießt dort, genauso wie die Funktion
? Ihr Graph nähert sich von rechts an die y-Achse an und schießt dort, genauso wie die Funktion 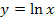 selbst, steil nach unten. Die Funktion
selbst, steil nach unten. Die Funktion 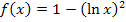 hat also ebenfalls die y-Achse als senkrechte Asymptote.
hat also ebenfalls die y-Achse als senkrechte Asymptote.
Die Gleichung der senkrechten Asymptote von 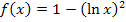 lautet:x = 0
lautet:x = 0
Zu 1d.)
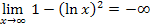
Erläuterung:
Es ist der Grenzwert der Funktion 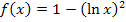 für
für  gesucht. Wir überlegen uns zuerst, wie sich die ln-Funktion
gesucht. Wir überlegen uns zuerst, wie sich die ln-Funktion 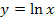 für
für  verhält. Die ln-Funktion wächst bekanntlich sehr langsam, aber ihre Funktionswerte nehmen dennoch mit zunehmenden x immer weiter zu. Die Funktion
verhält. Die ln-Funktion wächst bekanntlich sehr langsam, aber ihre Funktionswerte nehmen dennoch mit zunehmenden x immer weiter zu. Die Funktion 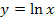 geht also für
geht also für  gegen Unendlich.
gegen Unendlich.

