Grenzwerte von e- und ln-Funktionen
Berechne die folgenden Grenzwerte!
a.) 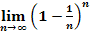
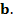 )
) 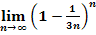
c.) 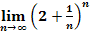
d.) 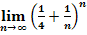
e.) 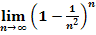
Hinweis:Die Grenzwerte 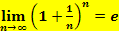 und
und 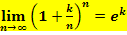 für k
für k  ℝ dürfen als bekannt vorausgesetzt werden.
ℝ dürfen als bekannt vorausgesetzt werden.
Lösung:
Zu 7a.)
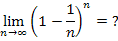
Wir bringen den gesuchten Grenzwert vorweg auf die Form 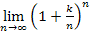 , indem wir das Minuszeichen in den Zähler des Bruchs schreiben.
, indem wir das Minuszeichen in den Zähler des Bruchs schreiben.
![]()
Nun lässt sich die Formel 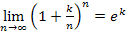 anwenden. Die Zahl -1 im Zähler des Bruchs in unserem gesuchten Grenzwert entspricht dem Buchstaben k aus dem bekannten Grenzwert
anwenden. Die Zahl -1 im Zähler des Bruchs in unserem gesuchten Grenzwert entspricht dem Buchstaben k aus dem bekannten Grenzwert 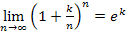 . Daher gilt:
. Daher gilt:
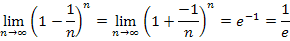
Zu 7b.)
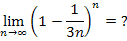
Wir bringen den Grenzwert wieder auf die Form 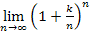 , indem wir das Minuszeichen und die Zahl
, indem wir das Minuszeichen und die Zahl  in den Zähler des Bruchs schreiben.
in den Zähler des Bruchs schreiben.
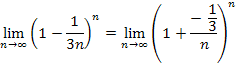
Die Zahl 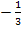 im Zähler des Bruchs entspricht dem Buchstaben k aus dem bekannten Grenzwert
im Zähler des Bruchs entspricht dem Buchstaben k aus dem bekannten Grenzwert 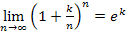 . Daher gilt:
. Daher gilt:
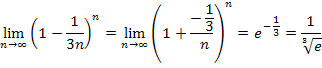
Zu 7c.)
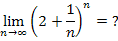
Bei diesem Grenzwert müssen wir gar nicht lange rechnen. Es lässt sich sofort erkennen, dass der Ausdruck innerhalb der Klammer für sehr große n gegen 2 geht. Jede Zahl, die größer ist als 1, wird unendlich groß, wenn man sie mit einer unendlich großen Zahl potenziert, also auch die Zahl 2. Es ist ja auch logisch, dass 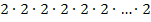 unendlich großwird, wenn man unendlich viele Zweier miteinander multipliziert. Es muss daher zwangsläufig gelten:
unendlich großwird, wenn man unendlich viele Zweier miteinander multipliziert. Es muss daher zwangsläufig gelten:
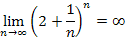
Du kannst dir das auch folgendermaßen klar machen: 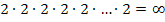
Zu 7d.)
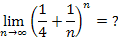
Auch bei diesem Grenzwert muss man nicht lange rechnen, um das Ergebnis zu bestimmen. Offensichtlich geht der Ausdruck innerhalb der Klammer für sehr große n gegen 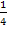 . Potenziert man eine positive Zahl, die kleiner ist als 1, mit einer unendlich großen Zahl, wird das Ergebnis immer kleiner, d.h. es geht gegen Null. Die Zahl
. Potenziert man eine positive Zahl, die kleiner ist als 1, mit einer unendlich großen Zahl, wird das Ergebnis immer kleiner, d.h. es geht gegen Null. Die Zahl 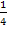 ist natürlich positiv und kleiner als 1. Die Zahl
ist natürlich positiv und kleiner als 1. Die Zahl 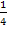 wird logischerweise immer kleiner, wenn man sie unendlich oft mit sich selbst multipliziert. Wir vermuten daher, dass der gesuchte Grenzwert gegen Null geht. Der Ausdruck
wird logischerweise immer kleiner, wenn man sie unendlich oft mit sich selbst multipliziert. Wir vermuten daher, dass der gesuchte Grenzwert gegen Null geht. Der Ausdruck 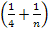 ist aber leider nicht exakt gleich
ist aber leider nicht exakt gleich 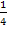 , sondern ein klein wenig größer. Mit einem kleinen Trick lässt sich jedoch ganz leicht zeigen, dass
, sondern ein klein wenig größer. Mit einem kleinen Trick lässt sich jedoch ganz leicht zeigen, dass 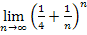 tatsächlich gegen Null geht. Ab
tatsächlich gegen Null geht. Ab 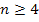 gilt nämlich:
gilt nämlich:
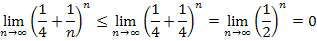
Multipliziert man die Zahl 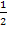 unendlich oft mit sich selbst, wird sie logischerweise immer kleiner. Es gilt deshalb:
unendlich oft mit sich selbst, wird sie logischerweise immer kleiner. Es gilt deshalb: 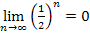
(Man kann dabei auch den bekannten Grenzwert der geometrischen Folge 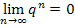 für
für 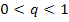 verwenden.)
verwenden.)
Weil ab 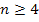 der Grenzwert
der Grenzwert 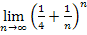 kleiner ist als
kleiner ist als 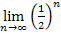 und außerdem
und außerdem 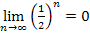 gilt, muss zwangsläufig auch
gilt, muss zwangsläufig auch 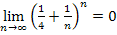 gelten.
gelten.
Zu 7e.)
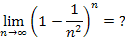
Um diesen Grenzwert zu bestimmen wenden wir vorweg die dritte binomische Formel 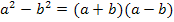 auf den Ausdruck innerhalb der Klammer an:
auf den Ausdruck innerhalb der Klammer an:
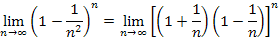
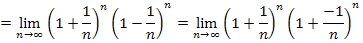
Nun können wir die Grenzwerte 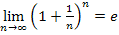 und
und 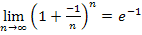 verwenden. Damit ergibt sich:
verwenden. Damit ergibt sich:
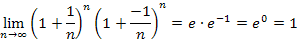
Damit ist diese Aufgabe gelöst. Es gibt noch viele interessante, d.h. schwierige Grenzwerte, die mit der Zahl e zu tun haben, doch würde das den Rahmen dieser website sprengen und außerdem sind sie für die Abiturprüfung sowieso nicht wirklich wichtig. (Wenn du dich für so etwas wirklich interessierst, dann solltest du Mathe studieren.) Die Grenzwerte, die in Abiturprüfungen tatsächlich verlangt werden, sind in der Regel deutlich einfacher als die im 7. Bsp. gezeigten Grenzwerte. Nur Aufgaben vom Schwierigkeitsgrad des 1. Bsp. bis zum 6. Bsp. sind abiturrelevant.
- Page 19 of 19
- « Previous
- 16
- 17
- 18
- 19
- Next »

