Grenzwerte von e- und ln-Funktionen
Altbekannte Schreibweise: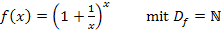 
Neue Schreibweise für Folgen: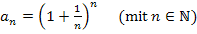 
Es gilt also im Folgenden grundsätzlich:n 
ℕ
Wir wollen uns jetzt überlegen, wie sich die Zahlenfolge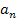 
für unendlich große Werte von n verhält. Schauen wir uns den Grenzwert 
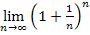also mal genauer an. Die Variable n steht für irgendeine natürliche Zahl, die gegen Unendlich gehen soll. Wir machen n also praktisch in einzelnen Schritten immer größer. Wir wollen also wissen, was passiert, wenn für n sehr große, ganze Zahlen eingesetzt werden.
Wenn n immer größer wird, wird der Bruch 
immer kleiner.
Man könnte also denken:Für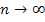 
gilt: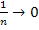 
Weil der Bruch gegen Null geht, gilt für 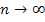logischerweise: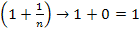 
Der Ausdruck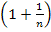 
geht demnach für 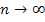gegen die Zahl 1. Das ist soweit noch korrekt. Weil die Zahl 1 hoch irgendeine Zahl genommen wieder 1 ergibt, könnte man auf die Idee kommen, dass auch 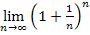gleich 1 sein. Genau das ist jedoch falsch!
Vorsicht: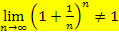 
Die Basis 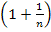der n.ten Potenz (d.h. der Ausdruck innerhalb der Klammer) geht zwar gegen 1, ist aber nicht exakt gleich 1. Da n zusätzlich im Exponenten steht, geht nämlich der Exponent gegen Unendlich und dann spielt es sehr wohl eine Rolle, dass die Basis nicht exakt 1 ist, sondern minimal größer. Es wird also eine Zahl, die minimal größer ist als 1, unendlich oft mit sich selbst multipliziert. Was kommt dabei heraus? Wir nehmen jetzt den Taschenrechner zu Hilfe und setzen einfach ein paar sehr große Zahlen für n ein. Du wirst sehen, dass dabei definitiv nicht ungefähr 1 herauskommt.
Was sich dabei für n = 10.000, n = 100.000 und für n = 1.000.000 wirklich ergibt, ist in der folgenden Tabelle zu sehen.
|
nDie Zahl e ist bekanntlich ungefähr 2,718281828. Je größer wir n machen, desto genauer nähern sich die Ergebnisse von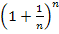 
an die Zahl e an. Es ist also zu vermuten, dass gilt:
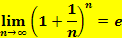
Diese Vermutung lässt sich auch streng mathematisch beweisen;der Beweis ist leider ziemlich aufwendig und die meisten Schüler sind bestimmt froh, wenn ihnen der Beweis erspart bleibt. Daher verzichten wir hier auf die Details dieses Beweises. Du brauchst das sowieso nicht für das Abitur.
Für den interessierten Schüler: Prinzip dieses Beweises
Des Weiteren lässt sich zeigen, dass gilt:
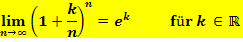
Auch auf den Beweis dieses Grenzwertes wollen wir hier verzichten. Du darfst die soeben erwähnten beiden Grenzwerte aber in den folgenden Aufgaben ohne weiteren Nachweis verwenden.
7. Bsp.:Grenzwerte der Form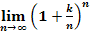 
mit n ℕ
