Grenzwerte von e- und ln-Funktionen

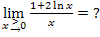
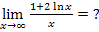
Wir beginnen mit dem Grenzwert für :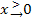

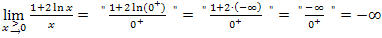
Senkrechte Asymptote:x = 0 (y-Achse)

Du schreibst den Grenzwert in Prüfungen am besten in der folgenden Form:

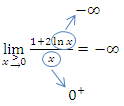
Dir ist nicht klar, wie man auf 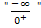kommt und warum das Endergebnis 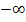ist? Erläuterung:Der Zähler geht insgesamt gegen Minus-Unendlich. Aber warum? Die ln-Funktion y = lnx geht bei Annäherung von rechts an x = 0 gegen Minus-Unendlich. (Erinnere dich an den Graph der ln-Funktion:Er hat die y-Achse x = 0 als senkrechte Asymptote und schießt bei Annäherung von rechts an x = 0 steil nach unten. Die ln-Funktion geht also für 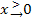gegen Minus-Unendlich.) Im Zähler ergibt sich also: 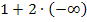„Zwei mal Minus-Unendlich“ ergibt praktisch wieder Minus-Unendlich. Die Zahl 1 kann man ignorieren;sie fällt gegenüber dem Minus-Unendlich nicht ins Gewicht. Ob man zu Minus-Unendlich noch 1 dazu zählt oder nicht, spielt fast keine Rolle. Die Zahl 1 kann vernachlässigt werden. Der Zähler geht deshalb insgesamt gegen Minus-Unendlich. Der Nenner geht natürlich gegen 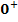. Insgesamt ergibt sich daher: 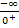Wie kommt man davon auf das Endergebnis? Ganz einfach:Zuerst schaut man sich bei 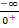nur die Vorzeichen an. Minus durch Plus ergibt natürlich wieder Minus. Also muss das Endergebnis negativ sein. Danach muss man sich fragen:Was ist 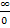? Teilen/Dividieren bedeutet nichts anderes, als sich zu überlegen, wie oft der Nenner in den Zähler passt. Die Division durch Null ist natürlich nicht definiert;wir schreiben hier zwar die Zahl Null in den Nenner, wir meinen mit dieser Null aber eigentlich eine Zahl, die nicht exakt gleich Null ist, sondern eine, die bloßfast Null ist. Es geht hierbei schließlich um einen Grenzwert! Du überlegst dir daher:Wie oft passt eine Zahl, die fast Null ist, also eine sehr kleine Zahl, in eine unendlich große Zahl hinein? Na klar, unendlich oft! Deshalb ist eine unendlich große Zahl geteilt durch eine Zahl, die fast Null ist, logischerweise wieder unendlich groß. In anderen Worten:Unendlich geteilt durch eine Zahl, die fast Null ist, wird erst recht unendlich groß. Eine sehr kleine Zahl passt schließlich sehr oft in eine unendlich große Zahl hinein und so kommst du auf: 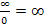Zusammen mit dem Vorzeichen „Minus“, das du dir schon vorher überlegt hast, ergibt sich als Endergebnis für den gesuchten Grenzwert .

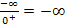Nun zum Verhalten von 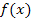im Unendlichen:

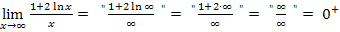
Begründung:Die ln-Funktion wächst langsamer als jede positive Potenz von x, also auch langsamer als 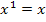. Daher wächst der Zähler langsamer als der Nenner und es gilt in diesem Fall:

---