Grenzwerte von e- und ln-Funktionen
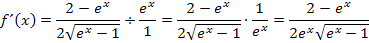
Weiter lässt sich die Ableitung nicht vereinfachen.
Wenn du Schwierigkeiten hattest, selbständig die Ableitung zu bilden, solltest du unbedingt den Teil Weitere Ableitungsregeln gründlich durcharbeiten.
Nun zu den gesuchten Grenzwerten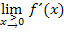 
und 
.
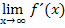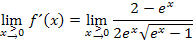
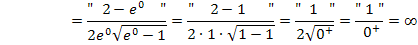
Anschaulich:Der Graph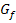 
hat an der Stelle x = 0 eine unendlich große Steigung, weil 
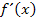schließlich der Steigung von 
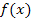entspricht. Die Tangente an 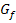bei x = 0 verläuft also senkrecht. D.h. der Graph beginnt quasi senkrecht steigend im Ursprung.
Dass die Funktion im Ursprung beginnt, kannst du leicht nachrechnen:
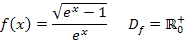
Wegen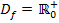 
ist der kleinste x-Wert, den wir einsetzen dürfen, logischerweise x = 0. Jetzt fehlt uns aber noch die zugehörige y-Koordinate 
.
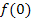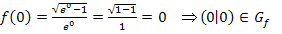
Der Graph 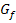beginnt im Ursprung und hat dort wegen 
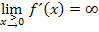eine senkrechte Tangente.
Beachte, dass die Funktion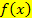 
an der Stelle x = 0 definiert ist, ihre Ableitung 
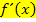jedoch nicht!
Vergleiche dazu die Definitionsmengen von 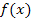und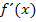 
:
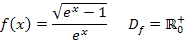
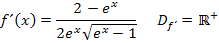
In die Ableitung 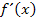kann man die Zahl 0 nicht einsetzen, weil dabei der Nenner Null ergeben würde. In die Funktion 
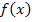selbst kann die Zahl 0 dagegen schon eingesetzt werden;der Nenner wird dabei nicht Null, sondern Eins.
Man kann zwar den Funktionswert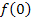 
berechnen, nicht aber die Ableitung 
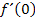. Ersatzweise wird deshalb der Grenzwert 
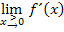ermittelt.
Nun zum Verhalten der Ableitung 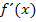für 
:
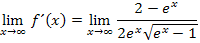
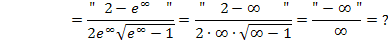
Nun stehen wir mal wieder vor dem Problem eines unbestimmten Ausdrucks. Wir müssen beurteilen, ob hier der Zähler oder der Nenner schneller wächst. Es ist zu vermuten, dass der Nenner schneller gegen Unendlich geht, weil im Nenner zusätzlich zu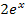 
auch noch 
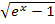einen Beitrag zum Unendlich liefert, im Zähler aber nur einmal 
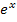vorkommt. Es ergibt sich deshalb aus 
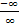insgesamt 
.
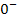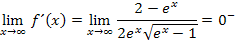
Anschaulich:Für wird die Steigung von 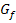fast Null. Der Graph verläuft für sehr große x nahezu waagrecht, was auch mit der oben herausgefundenen waagrechten Asymptote von 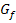für im Einklang steht. Am negativen Vorzeichen von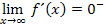 
erkennt man, dass der Graph fallend sein muss. Für fällt der Graph 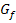also immer weniger;er schmiegt sich von oben kommend an seine waagrechte Asymptote, die x-Achse, an. Damit ist die Aufgabe gelöst.
Damit du dir das Ganze besser vorstellen kannst, hier noch zusätzlich der Graph der Funktion. (Die Zeichnung war natürlich in der Aufgabenstellung nicht verlangt.)
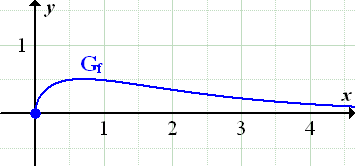
Abb.:Graph 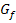der Funktion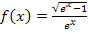 
Wegen 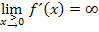verläuft die Tangente an 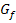im Ursprung senkrecht-steigend.
6. Bsp.:
Gib die maximale Definitionsmenge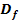 
der Funktion 
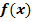an und untersuche das Verhalten von 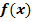an den Rändern des Definitionsbereichs!
