Grenzwerte von e- und ln-Funktionen
Der Ausdruck unter der Wurzel geht für 
gegen Null, ist aber nicht exakt Null. Der Bruch unter der Wurzel nähert sich also beliebig nah an die Null an, wenn x immer größer wird;er liefert für ein Ergebnis, das immer etwas größer ist als Null. Die Wurzel daraus ist dann selbst ebenfalls positiv, daher ergibt sich:
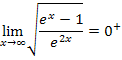
Bei den soeben beschriebenen Überlegungen haben wir praktisch die Reihenfolge von Grenzwert und Wurzel vertauscht. Wir haben uns schließlich zuerst den Grenzwert des Bruches überlegt und erst anschließend die Wurzel gezogen.
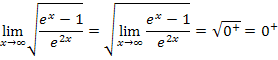
(Weil die Wurzelfunktion stetig ist, ist das Vertauschen der Reihenfolge von limes und Wurzel erlaubt. Das haben wir nicht näher besprochen, doch gibt es einen mathematischen Satz, der dies erlaubt. Du musst aber nicht mehr darüber wissen.)
Der Ausdruck unter der Wurzel geht zwar für gegen Null, ist aber nicht exakt Null. Der Bruch unter der Wurzel nähert sich also beliebig nah an die Null an, wenn x immer größer wird;er liefert für ein Ergebnis, das immer etwas größer ist als Null. Die Wurzel daraus ist dann selbst ebenfalls positiv, daher ergibt sich:
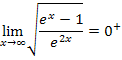
Zu 5b.)
Geg.: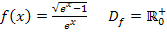 
Ges.: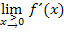 
und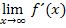 
Um die gesuchten Grenzwerte zu ermitteln, brauchen wir die erste Ableitung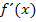 
. Wir leiten die Funktion also erst mal ab. Dazu verwenden wir die Quotientenregel, weil die Funktion die Variable x im Nenner enthält. Außerdem müssen wir innerhalb der Quotientenregel die Kettenregel anwenden, um die Ableitung des Zählers zu bilden, d.h. wir müssen nachdifferenzieren, wenn wir die Zählerableitung bilden.
Zur Erinnerung hier noch einmal die Quotientenregel:
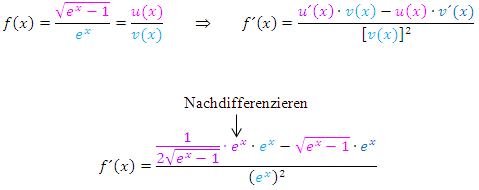
Die Ableitung muss natürlich noch vereinfacht werden. Wir klammern im Zähler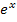 
aus;dadurch entsteht im Zähler ein Produkt und wir können den gesamten Bruch mit 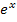kürzen.
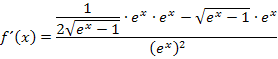
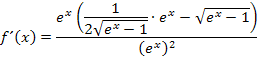
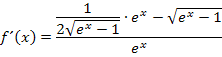
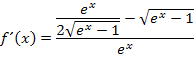
Im Zähler bringen wir jetzt alles auf einen gemeinsamen Bruchstrich. Der vordere Term im Zähler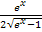 
hat den Nenner 
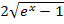;der hintere Term im Zähler 
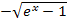ist gar kein Bruch. Wir denken ihn uns einfach als Bruch mit dem Nenner 1, also in der Form 
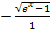. Wir bringen nun die beiden „Brüche“ im Zähler auf den gemeinsamen Nenner 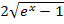. D.h. wir erweitern bei dem hinteren Term mit .
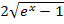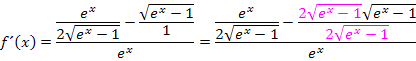
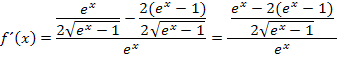
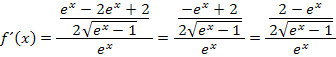
Als nächstes beseitigen wir den Doppelbruch. Wir denken uns an Stelle des 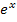, das ganz unten im Nenner steht, erst mal 
.
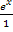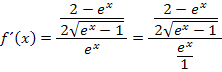
Den Hauptbruchstrich, also den längsten Bruchstrich, fassen wir nun als normales Geteilt-Zeichen auf.
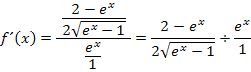
Weil man bekanntlich durch einen Bruch teilt, indem man mit dem Kehrwert multipliziert, rechnen wir nun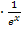 
statt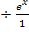 
.
