Definitionsmenge ermitteln bei e- und ln- Funktionen
Nun müssen wir noch die Gesamtdefinitionsmenge 
der Funktion 
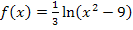angeben. Um die Gesamtdefinitionsmenge 
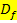zu erhalten, müssen die beiden Teildefinitionsmengen 
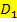und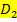 
vereinigt werden. Die Funktion ist schließlich definiert für alle Zahlen, die in 
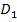oder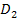 
liegen.
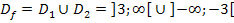
Wir vertauschen noch die Reihenfolge von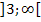 
und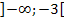 
, weil es schöner aussieht, wenn die Zahlenmenge mit den kleineren Zahlen (auf dem Zahlenstrahl weiter links) zuerst genannt wird.
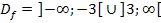
Es dürfen demnach bei 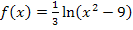alle reellen Zahlen für x eingesetzt werden, die entweder kleiner als -3 oder größer als 3 sind. Die Zahlen -3 und 3, sowie alle Zahlen dazwischen dürfen dagegen nicht eingesetzt werden. Es können somit alle reellen Zahlen eingesetzt werden ohne den Zahlen von -3 einschließlich bis 3 einschließlich. Die Zahlen -3 und 3 müssen beide aus der Definitionsmenge mitausgeschlossen werden, weil man -3 und 3 ja nicht in die Funktion einsetzen kann. An Stelle der Schreibweise 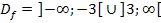kann man die Definitionsmenge daher auch kürzer schreiben:
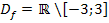
Die Schreibweise der Definitionsmenge mit dem Vereinigt-Zeichen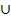 
in der Mitte ist nicht so elegant, daher ist dann die andere Schreibweise ℝ [...;...] zu bevorzugen. Die Schreibweise ℝ [...;...] wird aber wirklich nur dann angewendet, wenn die Definitionsmenge aus zwei getrennten Teilen 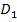und 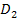besteht, die miteinander vereinigt sind.
2. Methode die quadratische Ungleichung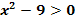 
zu lösen:Teils graphischer Weg
Schritt 1:
Ersetze das Ungleichheitszeichen durch ein Gleichheitszeichen und löse die dadurch entstandene quadratische Gleichung nach x auf!
Eine quadratische Gleichung lässt sich im Gegensatz zu einer quadratischen Ungleichung leicht lösen. Entweder einfach Wurzel ziehen, x ausklammern oder auf die Mitternachtsformel zurückgreifen. Die Mitternachtsformel brauchst du, wenn neben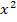 
auch noch x und eine Zahl in der Gleichung vorkommt. Das ist bei dieser Teilaufgabe jedoch nicht der Fall. Hier kann man einfach nach 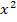auflösen und die Wurzel ziehen. Vorsicht:Plus / Minus nicht vergessen! (Mehr Informationen zum Lösen quadratischer Gleichungen im Teil: Rechnerische Lösungsverfahren quadratischer Gleichungen)
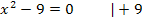
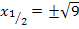
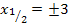
Warum das Plus/Minus? Ganz einfach:Wegen der geraden Potenz ergibt sich bei 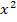die Zahl 9, wenn man entweder +3 oder -3 für x einsetzt. Du darfst also keinesfalls die negative Lösung -3 übersehen!
Schritt 2:
Wir fassen die quadratische Gleichung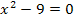 
als Nullstellenberechnung der Parabel 
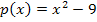auf.
