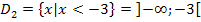Definitionsmenge ermitteln bei e- und ln- Funktionen
1. Fall:Beide Faktoren positiv oder 2. Fall:Beide Faktoren negativ
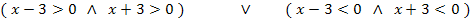
Am besten nimmst du jetzt einen Zahlenstrahl zu Hilfe, um herauszufinden, welche Zahlenbereiche jeweils beide Ungleichungen des 1. Falls zugleich bzw. beide Ungleichungen des 2. Falls zugleich erfüllen. Wir suchen jetzt also nach der Schnittmenge der beiden Mengen x >3 und x >-3 beim 1. Fall und nach der Schnittmenge der beiden Mengen x <3 und x <-3 beim 2. Fall.
Zum 1. Fall: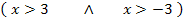 
Wir markieren den Zahlenbereich, der zur ersten Ungleichung x >3 gehört, zum Beispiel blau. Den Zahlenbereich, der zur zweiten Ungleichung x >-3 gehört, markieren wir in einer anderen Farbe, zum Beispiel rosa. Dann überlegen wir uns, welche Zahlen die erste und die zweite Ungleichung zugleich erfüllen. Wir suchen also den Bereich, der sowohl blau als auch rosa am Zahlenstrahl markiert ist. In anderen Worten:Wir müssen blau mit rosa schneiden. So finden wir den ersten Teil der Definitionsmenge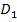 
.
Die Zahlen 3 und -3 sind dabei jeweils beide ausgeschlossen;du könntest das am Zahlenstrahl auch durch eckige Klammern andeuten, die nach außen gerichtet sind. Wir verzichten hier im Folgenden darauf.
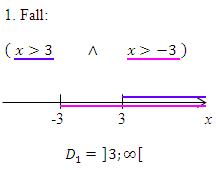
Zum 2. Fall: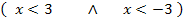 
Wir gehen entsprechend vor wie schon beim 1. Fall erläutert, aber an einem neuen Zahlenstrahl. Wir markieren den Zahlenbereich blau, der zur ersten Ungleichung x <3 gehört. Den Zahlenbereich, der zur zweiten Ungleichung x <-3 gehört, markieren wir rosa. Dann überlegen wir uns wieder, welcher Zahlenbereich die erste und die zweite Ungleichung zugleich erfüllt. Wir suchen also wieder denjenigen Bereich, der sowohl blau als auch rosa an diesem Zahlenstrahl markiert ist. In anderen Worten:Wir müssen wie schon beim 1. Fall blau mit rosa schneiden. So finden wir den zweiten Teil der Definitionsmenge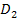 
.
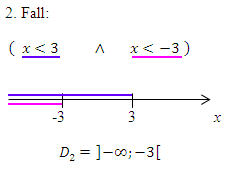
Anmerkung:
Wenn es dir zu viel Arbeit ist, jedes Mal einen Zahlenstrahl zu zeichnen, kannst du dir 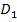und 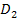natürlich auch ohne Zahlenstrahl nur im Kopf überlegen. An sich ist es ja klar, dass die beiden Ungleichungen des 1. Falls x >3 und x >-3 zugleich nur durch die Zahlen x >3 erfüllt werden können, denn jede Zahl über 3 ist gleichzeitig auch größer als -3. Deshalb gilt: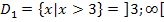 
Entsprechend kannst du dir 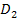auch folgendermaßen überlegen. Welche Zahlen erfüllen gleichzeitig die beiden Ungleichungen des 2. Falls x <3 und x <-3? Na klar, alle Zahlen für die gilt x <-3;denn eine Zahl unter -3 ist automatisch auch kleiner als 3. Deshalb gilt: 
