Definitionsmenge ermitteln bei e- und ln- Funktionen

Somit gilt:

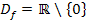
Zu 2d.)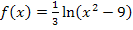

Gesucht:

Diese Teilaufgabe ist deutlich schwieriger zu lösen als die vorherigen. Das liegt daran, dass sich hier eine quadratische Ungleichung ergibt.

Wie du inzwischen sicher weißt, muss der Ausdruck, der hinter dem ln in der Klammer steht, d.h. in diesem Fall 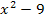, größer als Null sein. Wir müssen also die folgende Ungleichung lösen:

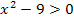
Das ist leider eine Ungleichung mit 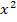, also eine quadratische Ungleichung und solche Ungleichungen lassen sich nicht so einfach lösen wie lineare Ungleichungen. (Lineare Ungleichungen sind Ungleichungen ohne 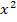und ohne x im Nenner, also ganz normale Ungleichungen, wie wir sie in den Teilaufgaben 2a. und 2b. hatten.) Doch wo ist denn hier das Problem?

Versuche doch gleich mal selbst die Ungleichung 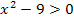zu lösen. Was würdest du machen?

Vermutlich hast du die Zahl 9 auf die rechte Seite der Ungleichung gebracht und dann versucht die Wurzel zu ziehen. (An Plus / Minus hast du natürlich gedacht.) Tja, dann ergibt sich aber leider ein Problem, nämlich das Ungleichheitszeichen. Dreht es sich um oder bleibt es, wie es ist? Die quadratische Gleichung 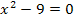lässt sich noch ganz leicht lösen;dabei ergibt sich logischerweise 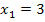und 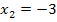. Aber was bei der Ungleichung 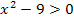herauskommt, kann man so leicht nicht sagen. Kommt dabei nun x >3, x >-3, x <3, x <-3 oder vielleicht -3 <x <3 heraus? Genau diese Frage lässt sich halt so einfach nicht beantworten. Also was tun?

Lösungsverfahren für quadratische Ungleichungen:

Es gibt für quadratische Ungleichungen einen rein rechnerischen und einen teils graphischen Lösungsweg. Es werden im Folgenden beide Lösungswege vorgeführt. Du musst aber nur einen davon beherrschen. Schau dir erst einmal beide Methoden an und suche dir dann den Weg aus, den du leichter findest. Mit diesem einen Lösungsweg kannst du dann in Zukunft alle anfallenden quadratischen Ungleichungen lösen.

1. Methode die quadratische Ungleichung 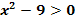zu lösen:Rein rechnerischer Weg

Wir faktorisieren die linke Seite der Ungleichung, d.h. wir formen die vorliegende Differenz 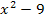in ein Produkt um. Hier geht das sehr leicht, weil sich die dritte binomische Formel anwenden lässt. (Wie man generell faktorisieren kann, wird erklärt bei:Faktorisierter Funktionsterm)

Zur Erinnerung hier die dritte binomische Formel: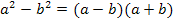

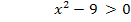
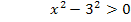
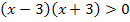
Nun liegt eine Ungleichung der Form:„Produkt >0“ vor. Bekanntlich ergibt Plus mal Plus wieder Plus, aber auch Minus mal Minus ergibt Plus. Daher ist ein Produkt größer Null, also positiv, wenn entweder beide Faktoren positiv sind oder beide negativ.

---