Definitionsmenge ermitteln bei e- und ln- Funktionen
Beide Schreibweisen sind gleichbedeutend. Achte aber darauf, dass die Zahl 
ausgeschlossen ist, d.h. die eckige Klammer in der Intervallschreibweise muss bei der Zahl nach außen zeigen. Wenn man für x einsetzen würde, ergäbe sich „ln0“ und das wäre nicht definiert. In der Ungleichung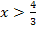 
steht schließlich das Größer-Zeichen 
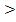und nicht das Größer/Gleich-Zeichen 
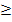. Daran erkennt man ebenfalls, dass wirklich nur Zahlen über für x eingesetzt werden dürfen, aber eben nicht die Zahl selbst.
Die eckige Klammer bei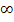 
ist ebenfalls nach außen gerichtet, da 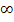keine richtige Zahl ist. Das ist nicht nur bei dieser Funktion so, sondern generell. Du kannst dir einfach merken, dass bei 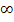oder auch 
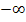die eckigen Klammern der Intervallschreibweise grundsätzlich nach außen zeigen. (Mehr zur Intervallschreibweise)
Zu 2b.)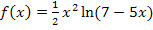 
Gesucht: 
Das Argument des ln muss positiv sein. Wir nehmen also den Ausdruck, der direkt hinter dem ln in der Klammer steht, d.h. hier den Ausdruck 7 – 5x und setzen ihn größer Null.
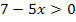
Dann lösen wir die Ungleichung. Dabei kannst du auf zwei etwas unterschiedliche Arten vorgehen:
1. Variante:
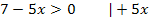
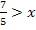
Es ist besser, wenn du bei Ungleichungen die Variable x auf die linke Seite stellst. Wir vertauschen also linke und rechte Seite der Ungleichung. Dabei dreht sich das Ungleichheitszeichen natürlich ebenfalls um.
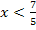
2. Variante:
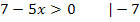
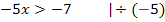
Beachte, dass sich bei der Division durch eine negative Zahl das Ungleichheitszeichen umdreht! (Das gleiche gilt auch für die Multiplikation mit einer negativen Zahl. Diese Regel heißt „Inversionsgesetz“. Bei der Addition oder Subtraktion einer beliebigen Zahl ändert sich jedoch nichts am Ungleichheitszeichen. Nur bei „geteilt durch eine Minus-Zahl“ oder bei „mal eine Minus-Zahl“ dreht sich das Ungleichheitszeichen um!) Weil hier durch -5 geteilt wird, dreht sich das Ungleichheitszeichen jetzt um:
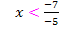
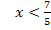
Die Funktion 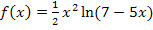ist folglich nur für Zahlen unter 
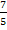definiert. Die Zahl 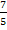selbst ist ausgeschlossen. Die Definitionsmenge lautet:
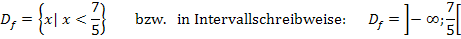
Zu 2c.)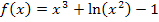 
Gesucht:
Das Argument des ln ist hier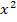 
. Bekanntlich kann 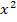wegen der geraden Potenz nicht negativ sein;es kann sich bei einer geraden Potenz nur eine positive Zahl oder Null ergeben. Der ln ist ausschließlich für positive Zahlen definiert. Daher darf man hier für x alle reellen Zahlen außer Null einsetzen. Die Zahl Null muss allerdings ausgeschlossen werden, denn für x = 0 würde sich bei 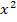nämlich 
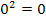ergeben, aber der ln von 0 ist nicht definiert.
