Definitionsmenge ermitteln bei e- und ln- Funktionen

Nenner = 0

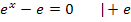
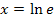
Mit 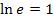ergibt sich:

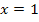
Wenn du für x die Zahl 1 in 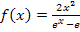einsetzen würdest, würde der Nenner 0 ergeben. Die Division durch Null ist aber nicht definiert;deshalb musst du die Zahl 1 aus der Definitionsmenge ausschließen. Es gilt somit für die Definitionsmenge:

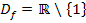
Zu 1g.)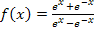

Gesucht:

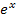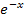Bei und kann man für x an sich alles einsetzen, aber der Nenner enthält ein x. Wir müssen also diejenigen Zahlen aus der Definitionsmenge ausschließen, für die der Nenner Null ergibt.

Nenner = 0

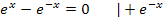
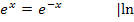
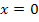
Wenn du für x die Zahl 0 in 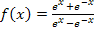einsetzen würdest, würde der Nenner 0 ergeben. Die Division durch Null ist aber nicht definiert;deshalb musst du die Zahl 0 aus der Definitionsmenge ausschließen. Es gilt somit für die Definitionsmenge:

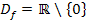
Zu 1h.)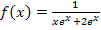

Gesucht:

Im Nenner der Funktion kommt die Variable x vor. Wir müssen also herausfinden, für welche Werte von x der Nenner gleich Null wird und diese Zahlen aus der Definitionsmenge ausschließen.

Nenner = 0

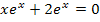
Wir klammern 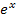aus:

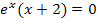
Nun liegt eine Gleichung der Form „Produkt gleich Null“ vor. Ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. Daher kann man die Faktoren einzeln gleich Null setzen. Der erste Faktor 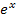kann niemals gleich Null werden; 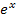ist schließlich immer größer Null. Deshalb können wir einfach nur den zweiten Faktor x + 2 gleich Null setzen. Offensichtlich wird die Gleichung x + 2 = 0 nur durch x = -2 gelöst.

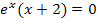
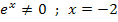
Nur für x = -2 wird der Nenner gleich Null;wir können also alle reellen Zahlen außer -2 für x einsetzen. Die Definitionsmenge ist folglich:

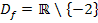
2. Bsp.:Definitionsmenge von ln-Funktionen

Gib die maximale Definitionsmenge der folgenden Funktionen an!

a.)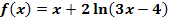

b.)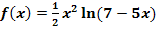

c.)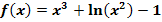

d.)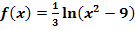

e.)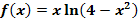

f.)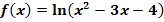

g.)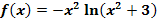

h.)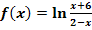

i.)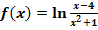

j.)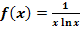

k.)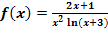

Lösung:

Zu 2a.)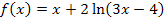

Gesucht:

Das Argument des ln (also der Ausdruck in der Klammer direkt hinter dem ln, in diesem Fall 3x - 4) muss größer als Null sein, damit der ln definiert ist. In anderen Worten:ln von negativen Zahlen oder ln von Null gibt es nicht, weil das nicht definiert ist! Hinter dem ln muss etwas Positives stehen. Deshalb muss folgende Ungleichung erfüllt sein, damit der ln hier definiert ist:

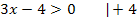
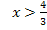
Nur für Zahlen größer als ist die Funktion definiert. Die Definitionsmenge lautet folglich:

Welche Schreibweise du verwendest, ist reine Geschmackssache.

---