Definitionsmenge ermitteln bei e- und ln- Funktionen
Bei Funktionen mit x im Nenner ist es sinnvoll, vorweg genau diejenigen Zahlen auszurechnen, die man eben nicht in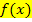 
einsetzen darf, weil dann der Nenner Null ergeben würde. Diese Zahlen muss man dann aus der Definitionsmenge ausschließen. Es gibt schließlich nur ein paar ganz bestimmte Zahlen, für die der Nenner Null wird. Genau diese wenigen Zahlen berechnet man also zuerst, indem man den Nenner gleich Null setzt, und schließt sie dann aus der Definitionsmenge aus. Bei Funktionen mit x im Nenner berechnet man also die Definitionslücken. Die Definitionsmenge ist dann ℝ ohne die Definitionslücke(n), mathematisch geschrieben: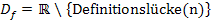 
Bei Wurzelfunktionen geht man anders vor:Man berechnet gleich von vornherein, welche Zahlen in 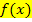eingesetzt werden dürfen. Man nimmt also den Ausdruck unter der Wurzel, setzt ihn größergleich Null und löst nach x auf. Das liefert direkt die Definitionsmenge. Warum sollte man bei Wurzelfunktionen auch erst diejenigen Zahlen suchen, für welche die Funktion nicht definiert ist und diese dann wieder ausschließen. Das wäre wesentlich komplizierter, da hier nicht einzelne Zahlen, sondern ein ganzer Zahlenbereich auszuschließen wäre. Bei Wurzelfunktionen gibt es eben keine einzelnen Definitionslücken, also keine vereinzelten Zahlen, die man nicht für x einsetzen kann, sondern ein ganzes Intervall von Zahlen, die nicht eingesetzt werden können. Daher ist es bequemer direkt denjenigen Zahlenbereich zu berechnen, für den die Funktion definiert ist. Man rechnet also ohne Umweg gleich die Definitionsmenge aus.
Bei ln-Funktionen geht man ähnlich vor wie bei den Wurzelfunktionen. Auch bei Funktionen mit ln rechnet man direkt die Definitionsmenge aus. Man nimmt das Argument des ln (also den Ausdruck, auf den sich der ln bezieht) und setzt ihn größer Null. Dann löst man die Ungleichung nach x auf. Das liefert sofort die Definitionsmenge. Auch hier werden also nicht zuerst diejenigen Zahlen gesucht, die man bei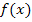 
für x nicht einsetzen darf, sondern gleich diejenigen, die man tatsächlich einsetzen kann. Kommt bei einer Funktion mit ln außerdem x im Nenner vor, müssen natürlich des Weiteren diejenigen Zahlen ausgeschlossen werden, für die der Nenner Null ergeben würde. Mehr dazu im 2. Bsp.
Zu 1f.)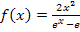 
Gesucht: 
Bei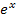 
kann man für x an sich alles einsetzen, aber der Nenner enthält ein x. Wir müssen uns daher fragen, ob der Nenner gleich Null werden kann. Der Nenner 
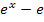hat die Form 
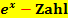und solche Ausdrücke können, im Gegensatz zu 
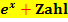, sehr wohl gleich Null werden. Wir müssen daher herausfinden, für welche Zahl der Nenner Null ergibt, und diese Zahl aus der Definitionsmenge ausschließen.
