Definitionsmenge ermitteln bei e- und ln- Funktionen
Ein Ausdruck der Form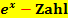 
kann nämlich schon gleich Null oder negativ sein. BloßAusdrücke der Form 
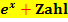ergeben grundsätzlich positive Werte und sind somit nie gleich Null. Deshalb ist der Nenner 
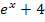immer ungleich Null.
Folgerung:Es handelt sich bei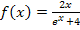 
zwar um eine Funktion mit x im Nenner, aber der Nenner 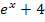kann gar nicht Null ergeben. Daher kann man jede beliebige reelle Zahl für x einsetzen. Die Definitionsmenge lautet:
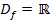
Auf das gleiche Ergebnis kommst du natürlich auch, wenn du den Nenner 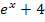gleich Null setzt und versuchst nach x aufzulösen. Du wirst sehen, dass es kein x gibt, welches die folgende Gleichung erfüllt:
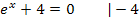
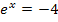
Um nach x im Exponenten aufzulösen, müsstest du eigentlich den ln verwenden. Weil der ln aber nur für positive Argumente definiert ist, kann man den ln von -4 nicht berechnen. In anderen Worten:„ln(-4)“ gibt es nicht! ln(-4) darf man eigentlich gar nicht hinschreiben. Weil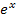 
nur positiv sein kann, kann die Gleichung 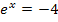keine Lösung haben und ln(-4) gibt es nicht. Der Nenner der Funktion 
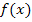, also der Ausdruck 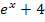, ist nie gleich Null. Wir brauchen somit keine Zahl aus der Definitionsmenge ausschließen. Die Funktion ist für alle reellen Zahlen definiert.
Zu 1e.)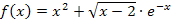 
Gesucht: 
Um die Definitionsmenge dieser Funktion zu ermitteln, muss der Radikand (= Ausdruck unter der Wurzel) größer oder gleich Null sein. Wie du weißt, darf unter einer Wurzel nichts Negatives stehen. Wir müssen deshalb ermitteln, für welche Werte von x der Ausdruck x – 2 größer oder gleich Null ist. Das kannst du dir entweder im Kopf überlegen oder schriftlich die folgende Ungleichung lösen:
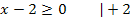
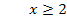
Die Funktion ist also für alle Werte größer oder gleich 2 definiert. Zahlen unter 2 kann man nicht einsetzen, denn dann würde sich unter der Wurzel eine negative Zahl ergeben. (Probiere es doch einfach mal aus, eine Zahl kleiner 2 einzusetzen, zum Beispiel 1. Dann ergibt sich unter der Wurzel 1 – 2 = – 1 also etwas Negatives und daraus kann man die Wurzel nicht ziehen.) Die Definitionsmenge lautet:
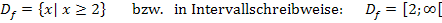
Welche Schreibweise du verwendest, ist reine Geschmackssache. Beide Schreibweisen sind gleichbedeutend. (Genaueres zur Intervallschreibweise)
Anmerkung:Anders als bei Funktionen, die x im Nenner enthalten, rechnet man bei Funktionen, die eine Wurzel mit x darunter enthalten, nicht zuerst diejenigen Zahlen aus, die man nicht für x einsetzen darf und schließt diese Zahlen dann wieder aus, sondern man ermittelt sofort diejenigen Zahlen, die man einsetzen kann.
