Definitionsmenge ermitteln bei e- und ln- Funktionen
1. Bsp.:Definitionsmenge von e-Funktionen
Gib die maximale Definitionsmenge der folgenden Funktionen an!
a.) 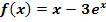
b.) 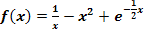
c.) 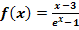
d.) 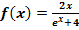
e.) 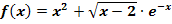
f.) 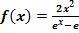
g.) 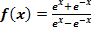
h.) 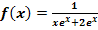
Lösung:
Zu 1a.) 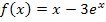
Gesucht: 
Da die Funktion weder einen Logarithmus, noch eine Wurzel und auch kein x im Nenner hat (überhaupt kein Bruch vorhanden), kann man beliebige reelle Zahlen für x einsetzen. 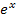 ist schließlich für x
ist schließlich für x  ℝ definiert. Die gesuchte Definitionsmenge lautet:
ℝ definiert. Die gesuchte Definitionsmenge lautet:
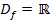
Zu 1b.) 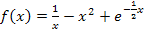
Gesucht: 
Bei 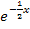 kann man zwar jede beliebige reelle Zahl für x einsetzen, aber nicht bei
kann man zwar jede beliebige reelle Zahl für x einsetzen, aber nicht bei  . Bei dem Ausdruck
. Bei dem Ausdruck  steht die Variable x im Nenner;der Nenner darf jedoch nicht Null ergeben. Daher kann die Zahl 0 nicht für x eingesetzt werden. Folglich kann man „Alles außer 0“ für x einsetzen. (Mit „Alles“ sind „alle reellen Zahlen gemeint, da wir in der Oberstufe grundsätzlich mit der Grundmenge ℝ rechnen.) Es gilt somit für die Definitionsmenge:
steht die Variable x im Nenner;der Nenner darf jedoch nicht Null ergeben. Daher kann die Zahl 0 nicht für x eingesetzt werden. Folglich kann man „Alles außer 0“ für x einsetzen. (Mit „Alles“ sind „alle reellen Zahlen gemeint, da wir in der Oberstufe grundsätzlich mit der Grundmenge ℝ rechnen.) Es gilt somit für die Definitionsmenge:
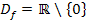
Zu 1c.) 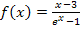
Gesucht: 
Bei 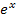 kann man zwar jede beliebige reelle Zahl für x einsetzen, aber der Nenner
kann man zwar jede beliebige reelle Zahl für x einsetzen, aber der Nenner 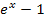 darf nicht gleich 0 werden.
darf nicht gleich 0 werden.
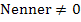
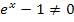
Mit einem Ungleichheitszeichen rechnet es sich aber schlecht. Wir rechnen daher vorweg einfach aus, für welchen Wert (bzw. für welche Werte) von x der Nenner genau 0 ergeben würde. D.h. wir setzen den Nenner gleich 0, lösen nach x auf und schließen bei der Definitionsmenge den berechneten Wert (bzw. die berechneten Werte) dann einfach wieder aus.
Nenner = 0
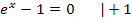

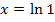
Wegen 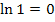 ergibt sich:
ergibt sich:
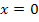
Wenn du für x die Zahl 0 in 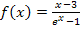 einsetzen würdest, würde der Nenner 0 ergeben. Die Division durch Null ist aber nicht definiert;deshalb musst du die Zahl 0 aus der Definitionsmenge ausschließen. Es gilt somit für die Definitionsmenge:
einsetzen würdest, würde der Nenner 0 ergeben. Die Division durch Null ist aber nicht definiert;deshalb musst du die Zahl 0 aus der Definitionsmenge ausschließen. Es gilt somit für die Definitionsmenge:
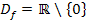
Zu 1d.) 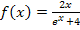
Gesucht: 
Bei dieser Funktion kann man die Definitionsmenge auch ohne jegliche Rechnung erkennen. Bei 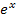 kann man jede beliebige reelle Zahl für x einsetzen. Zu beachten ist allerdings, dass der Nenner der Funktion die Variable x enthält. Du musst dir deshalb überlegen, ob der Nenner
kann man jede beliebige reelle Zahl für x einsetzen. Zu beachten ist allerdings, dass der Nenner der Funktion die Variable x enthält. Du musst dir deshalb überlegen, ob der Nenner 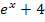 gleich Null werden kann. Das kann er aber nicht, denn
gleich Null werden kann. Das kann er aber nicht, denn 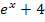 ist immer positiv, also größer Null und niemals gleich Null! Woher weißman das? Der Ausdruck
ist immer positiv, also größer Null und niemals gleich Null! Woher weißman das? Der Ausdruck 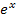 ist grundsätzlich positiv, was du auch daran erkennst, dass der Graph der Funktion
ist grundsätzlich positiv, was du auch daran erkennst, dass der Graph der Funktion 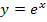 nur oberhalb der x-Achse verläuft. Wenn
nur oberhalb der x-Achse verläuft. Wenn 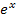 schon positiv ist, muss
schon positiv ist, muss 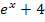 erst recht positiv sein. Wenn man zu einer positiven Zahl etwas dazuzählt, wird es ja noch größer.
erst recht positiv sein. Wenn man zu einer positiven Zahl etwas dazuzählt, wird es ja noch größer.
Vorsicht:Hätte 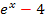 oder
oder 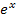 minus irgendeine andere Zahl im Nenner gestanden, hätten wir nicht so argumentieren können.
minus irgendeine andere Zahl im Nenner gestanden, hätten wir nicht so argumentieren können.

