Definitionsmenge ermitteln bei e- und ln- Funktionen
2. Nebenrechnung:
Nenner = 0
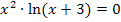
Es liegt eine Gleichung der Form „Produkt = 0“ vor. Wir setzen die einzelnen Faktoren gleich Null.
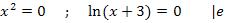
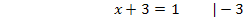
Aus den beiden Überlegungen folgt somit, dass x größer sein muss als -3 und nicht 0 oder -2 sein darf. Die Definitionsmenge der Funktion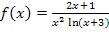 
lautet also:
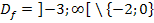
Zum Abschluss noch ein kleiner Hinweis zu der mathematischen Schreibweise dieser Definitionsmenge.
Die eckigen Klammern stehen immer für ein ganzes Intervall von einer Zahl bis zu einer anderen (oder Unendlich). Zeigt die eckige Klammer nach außen von der Zahl weg, so ist diese Zahl ausgeschlossen. Unendlich bzw. Minus-Unendlich werden grundsätzlich ausgeschlossen. (Mehr dazu bei:Intervallschreibweise)
Die geschweiften Klammern verwendet man dagegen, wenn man einzelne Zahlen aufzählen will.
Deshalb beschreibt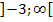 
die Menge aller Zahlen von -3 (ausgeschlossen) bis Unendlich.
Mit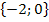 
sind nur die Zahlen -2 und 0 gemeint, nicht aber die Zahlen dazwischen.
Sollen eine oder mehrere Zahlen oder sogar ein ganzer Zahlenbereich ausgeschlossen werden, verwendet man in der Mathematik das „Ohne-Zeichen“;d.h. das Zeichen . Hinter das Zeichen wird die Zahl bzw. die Menge von Zahlen geschrieben, die ausgeschlossen werden soll.
Deshalb beschreibt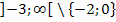 
die Menge aller Zahlen von -3 bis Unendlich ohne den Zahlen -2 und 0.
Die gezeigten Beispielen zur Ermittlung der Definitionsmenge von e- bzw. ln-Funktionen sollen uns an dieser Stelle genügen. Im Abschnitt Komplette Kurvendiskussion bei e- und ln-Funktionen findest du aber noch weitere Beispiele dazu;fast jede Kurvendiskussion beginnt ja mit der Ermittlung der Definitionsmenge, außer sie ist bereits angegeben. Ohne korrekte Definitionsmenge kannst du nicht die richtigen Grenzwerte bei der Untersuchung des Verhaltens an den Rändern der Definitionsmenge berechnen. Deshalb ist es so wichtig, dass du die Definitionsmenge korrekt ermitteln kannst.
