Definitionsmenge ermitteln bei e- und ln- Funktionen

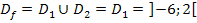
Zu 2i.)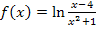

Gesucht:

Das Argument des natürlichen Logarithmus 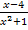muss positiv sein. Es muss daher gelten:

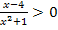
Diese Ungleichung enthält ein x im Nenner;es handelt sich daher wie auch in Teilaufgabe 2h. um eine Bruchungleichung.

Eine Ungleichung der Form „Bruch >0“ wird gelöst, indem man die folgenden zwei Fälle unterscheidet:Entweder müssen Zähler und Nenner beide größer Null sein oder beide gleichzeitig negativ. (Plus durch Plus ergibt schließlich wieder Plus, aber auch Minus durch Minus ergibt Plus.) Nun schau dir mal den Nenner 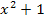genauer an und überlege dir dessen Vorzeichen. Du hast es bestimmt selbst gemerkt:In unserer Ungleichung kann der Nenner gar nicht negativ werden, weil 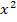wegen der geraden Potenz niemals negativ wird, wird 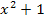erst recht nicht negativ. Wenn man zu 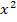etwas dazuzählt, kommt nämlich immer etwas Positives heraus. Deshalb gilt für x ℝ: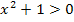

Deshalb brauchen wir den Fall „beide Faktoren negativ“ gar nicht durchrechnen;es würde sowieso nicht gehen. Es bleibt hier also nur der Fall „beide Faktoren positiv“.

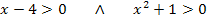
Das Argument des natürlichen Logarithmus 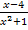ist somit positiv für alle reellen Zahlen, die größer sind als 4. Daher lautet die Definitionsmenge der Funktion :

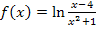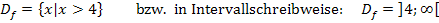
Zu 2j.)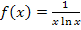

Gesucht:

Bei dieser Funktion sind zwei Dinge zu beachten:

1. Das Argument des ln muss positiv sein, d.h. es muss hier auf jeden Fall gelten:x >0

2. Der Nenner des Bruchs darf nicht gleich Null werden.

Um herauszufinden, für welche Werte von x der Nenner gleich Null wird, machen wir eine kleine Nebenrechnung:

Nenner = 0

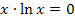
Ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. wir können die Faktoren einzeln gleich Null setzen. Das ergibt:

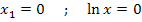
Bekanntlich gilt: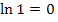

Somit ergibt sich:

Anmerkung:Die Gleichung 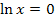hättest du auch folgendermaßen lösen können:

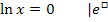
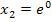
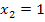
Weil man bei lnx sowieso nur positive Werte für x einsetzen darf, ist 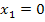sowieso schon ausgeschlossen. Der Nenner würde aber auch für 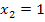Null ergeben, daher muss die Zahl 1 auf jeden Fall noch ausgeschlossen werden.

Die gesuchte Definitionsmenge der Funktion 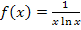lautet: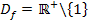

Zu 2k.)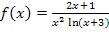

Gesucht:

Ähnlich wie auch in Teilaufgabe 2j. ist zu beachten, dass das Argument des ln positiv sein muss und dass außerdem der Nenner der Funktion nicht gleich Null werden darf.

Bei 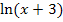darf man nur Werte für x einsetzen, die größer sind als -3. Das folgt aus der Ungleichung x + 3 >0.

1. Nebenrechnung:

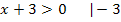
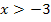
Nun gilt es noch herauszufinden, für welche Werte der Nenner Null ergeben würde. Diese Werte sind dann noch auszuschließen.

---