Definitionsmenge ermitteln bei e- und ln- Funktionen

(Wenn eine Parabel keine Nullstellen hat und nach oben geöffnet ist, liegt sie zwangsläufig komplett oberhalb der x-Achse.) Auch daran kann man erkennen, dass die Ungleichung 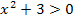für jede beliebige reelle Zahl x erfüllt ist.

Zu 2h.)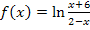

Gesucht:

Das Argument des natürlichen Logarithmus 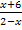muss positiv sein. Es muss daher gelten:

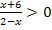
Diese Ungleichung enthält ein x im Nenner;es handelt sich daher um eine Bruchungleichung. Weißt du, wie man so eine Ungleichung lösen kann?

Vermutlich würdest du hier einfach mit dem Nenner 2 – x multiplizieren, doch was passiert dann mit dem Ungleichheitszeichen? Dreht es sich um oder nicht? Das hängt bekanntlich davon ab, ob man mit etwas Negativem oder mit etwas Positiven multipliziert. (Vergleiche:Inversionsgesetz) Leider hängt das Vorzeichen von 2 – x davon ab, was man für x einsetzt, also ob x größer oder kleiner ist als 2. (Die Zahl 2 selbst kann man nicht einsetzen, weil der Nenner für x = 2 Null ergeben würde. Die Division durch Null ist ja nicht definiert.) Daher ist eine Fallunterscheidung notwendig.

Es liegt hier eine besondere Art von Bruchgleichung vor, nämlich eine Ungleichung der Form:„Bruch >0“

Solche Bruchungleichungen lassen sich besonders einfach lösen. Du weißt, dass ein Bruch positiv ist, wenn Zähler und Nenner beide das gleiche Vorzeichen haben. (Plus durch Plus ergibt schließlich wieder Plus, aber auch Minus durch Minus ergibt Plus.)

Wir müssen deshalb die folgenden zwei Fälle unterscheiden:Zähler und Nenner beide gleichzeitig größer Null, oder Zähler und Nenner beide gleichzeitig kleiner Null.

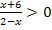
1. Fall: oder        2. Fall:

Zähler und zugleich Nenner positiv Zähler und zugleich Nenner negativ

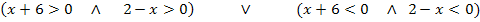
Am Zahlenstrahl kannst du die beiden Teildefinitionsmengen 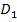und 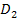, die sich aus dem ersten bzw. aus dem zweiten Fall ergeben, leicht ablesen. Man muss dazu jeweils beim ersten und beim zweiten Fall denjenigen Bereich suchen, der am Zahlenstrahl blau und zugleich rosa markiert ist, d.h. jeweils die beiden farbigen Bereiche miteinander schneiden. (Beim zweiten Fall gibt es hier so einen Bereich gar nicht, da sich der blau markierte Bereich mit dem rosa markierten Bereich nicht überlappt. Ist ja auch klar, denn es gibt keine Zahl, die kleiner ist als -6 und gleichzeitig größer ist als 2. 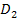ist deshalb hier die leere Menge.)

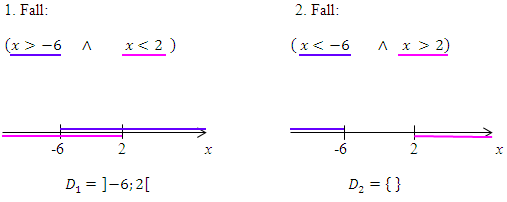
Um die Gesamtdefinitionsmenge 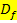zu erhalten, müssen normalerweise die beiden Teildefinitionsmengen 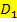und 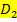vereinigt werden. Da hier jedoch 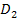die leere Menge ist, entspricht 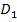direkt der Gesamtdefinitionsmenge .

---