Definitionsmenge ermitteln bei e- und ln- Funktionen
Mit Hilfe der Nullstellen x = 4 und x = -1 skizzieren wir die Parabel nun ganz grob. Es kommt dabei wieder vor allem darauf an, ob die Parabel nach oben oder nach unten geöffnet ist. Die Parabel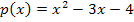 
ist nach oben geöffnet, weil vor dem 
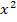quasi ein Plus steht. (Für a >0 sind die Graphen von Funktionen der Form 
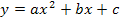nach oben geöffnete Parabeln. Mehr dazu bei:Parabeln zeichnen) Die Breite der Parabel ist für die Skizze an sich nebensächlich. Bei 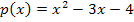handelt es sich allerdings um eine nach oben geöffnete Normalparabel, da die Zahl vor dem 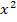gleich 1 ist. Siehe Abbildung!
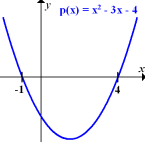
Abb.:Skizze der nach oben geöffneten Parabel 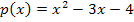mit ihren Nullstellen x = 4 und x = -1
Aus der Skizze kann man dann ablesen, für welche x die Ungleichung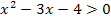 
erfüllt ist. Dazu musst du bloßschauen, wo die Parabel oberhalb der x-Achse verläuft, und die entsprechenden Bereiche auf der x-Achse aus der Zeichnung ablesen. Das ergibt direkt die Lösung der Ungleichung 
.
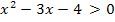In der folgenden Abbildung sind die entsprechenden Bereiche der Parabel hellblau markiert und die gesuchten Bereiche auf der x-Achse rot.
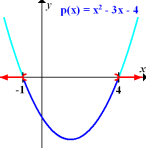
Abb.:Zur graphischen Lösung von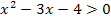
Aus der Zeichnung lesen wir jetzt ab: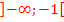 
sowie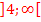 
Alle Zahlen, die im Intervall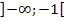 
oder im Intervall 
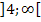liegen, erfüllen somit die Ungleichung 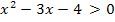. Die beiden Mengen müssen daher vereinigt werden. Dadurch ergibt sich die gesuchte Definitionsmenge der Funktion 
.
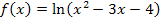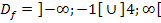
An Stelle der Schreibweise 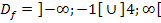kann man natürlich auch wieder schreiben:
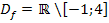
Zu 2g.)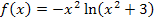 
Gesucht: 
Das Argument des natürlichen Logarithmus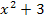 
muss positiv sein. Es muss daher gelten:
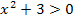
Diese Ungleichung ist immer wahr, da eine gerade Potenz niemals negativ werden kann. Wenn man zu einer geraden Potenz etwas dazuzählt, ergibt sich immer etwas Positives. 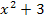ist immer positiv, egal für welches x. D.h. die Ungleichung 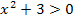wird durch alle reellen Zahlen erfüllt. Wir brauchen also gar nichts zu rechnen. Die Definitionsmenge ist einfach: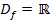 
Wenn du versucht hättest die Ungleichung nach dem oben beschriebenen rein rechnerischen Verfahren zu lösen, hättest du festgestellt, dass sich der Term 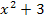nicht faktorisieren lässt, weil er niemals gleich Null werden kann. Wird ein Term nicht gleich Null, kann man ihn auch nicht faktorisieren;man kann ihn also gar nicht als Produkt schreiben. Hättest du es mit dem graphischen Lösungsweg versucht, hättest du ebenfalls das Problem gehabt, dass der Term 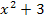nicht Null ergibt. Die Parabel 
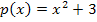hat keine Nullstellen;sie liegt immer oberhalb der x-Achse.
