Definitionsmenge ermitteln bei e- und ln- Funktionen

(Ausführlichere Erklärungen zum Faktorisieren bei:Faktorisierter Funktionsterm)

Faktorisieren des Terms :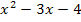

• Term gleich Null setzen:

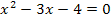
• Mitternachtsformel anwenden:

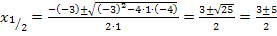
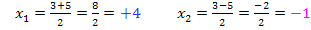
• Faktorisierung:

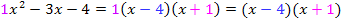
Nun können wir statt 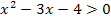auch Folgendes schreiben:

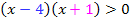
Die vorliegende Ungleichung hat die Form „Produkt >0“ und ein Produkt ist bekanntlich größer Null, wenn beide Faktoren dasselbe Vorzeichen haben, also beide gleichzeitig Plus oder beide gleichzeitig Minus sind.

1. Fall:Beide Faktoren positiv        oder       2. Fall:Beide Faktoren negativ

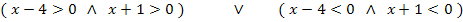
Wir müssen jetzt beim 1. Fall die Schnittmenge der beiden Mengen x >4 und x >-1 bilden und beim 2. Fall die Schnittmenge der beiden Mengen x <4 und x <-1. Du kannst dazu wieder jeweils einen Zahlenstrahl zu Hilfe nehmen.

Zum 1. Fall: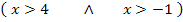

Markiere denjenigen Zahlenbereich z. B. in Blau, der zur ersten Ungleichung x >4 gehört. Den Zahlenbereich, der zur zweiten Ungleichung x >-1 gehört, markierst du in einer anderen Farbe z.B. mit Rosa. Dann musst du die beiden Bereiche miteinander schneiden. Du nimmst also den Bereich, der sowohl blau als auch rosa am Zahlenstrahl markiert ist. Das ist der erste Teil der Definitionsmenge .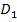

Die Zahlen 4 und -1 sind dabei jeweils beide ausgeschlossen;du könntest das am Zahlenstrahl auch durch eckige Klammern andeuten, die nach außen gerichtet sind. Wir verzichten hier darauf.

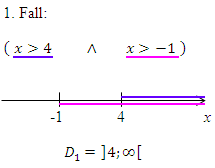
Zum 2. Fall: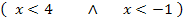

Nimm einen zweiten Zahlenstrahl und markiere den Zahlenbereich in Blau, der zur ersten Ungleichung x <4 gehört. Den Zahlenbereich, der zur zweiten Ungleichung x <-1 gehört, markierst du z. B. mit Rosa. Dann nimmst du wieder denjenigen Bereich, der sowohl blau als auch rosa an diesem Zahlenstrahl markiert ist. Das ergibt dann den zweiten Teil der Definitionsmenge .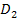

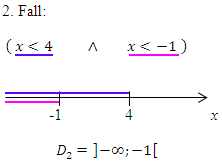
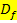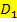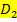Um die Gesamtdefinitionsmenge zu erhalten, müssen die beiden Teildefinitionsmengen und vereinigt werden.

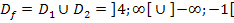
Schöner sieht es aus, wenn man die Reihenfolge noch umdreht:

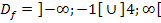
An Stelle der Schreibweise 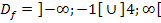kann man die Definitionsmenge auch kürzer schreiben:

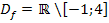
Diese Schreibweise ist hier die eleganteste.

2. Methode die quadratische Ungleichung 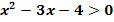zu lösen:Teils graphischer Weg

Schritt 1:

Wir ersetzen das Ungleichheitszeichen durch ein Gleichheitszeichen und lösen die so entstandene quadratische Gleichung nach x auf! Dabei verwenden wir die Mitternachtsformel:

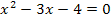
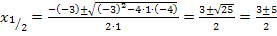
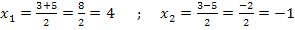
Schritt 2:

Wir fassen die quadratische Gleichung 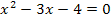als Nullstellenberechnung der Parabel 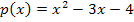auf.

---