Definitionsmenge ermitteln bei e- und ln- Funktionen
Dann überlegen wir uns, welche Zahlen die erste und die zweite Ungleichung zugleich erfüllen. Wir suchen also den Bereich, der sowohl blau als auch rosa am Zahlenstrahl markiert ist. In anderen Worten:Wir müssen blau mit rosa schneiden. So finden wir den ersten Teil der Definitionsmenge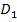 
.
Die Zahlen 2 und -2 sind dabei jeweils beide ausgeschlossen;du könntest das am Zahlenstrahl auch durch eckige Klammern andeuten, die nach außen gerichtet sind. Wir verzichten hier darauf.
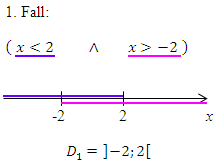
Zum 2. Fall: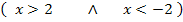 
Wir nehmen einen zweiten Zahlenstrahl und markieren den Zahlenbereich blau, der zur ersten Ungleichung x >2 gehört. Den Zahlenbereich, der zur zweiten Ungleichung x <-2 gehört, markieren wir rosa. Dann überlegen wir uns wieder, welcher Zahlenbereich die erste und die zweite Ungleichung zugleich erfüllt. Wir suchen also wieder denjenigen Bereich, der sowohl blau als auch rosa an diesem Zahlenstrahl markiert ist. In anderen Worten:Wir müssen wie schon beim 1. Fall blau mit rosa schneiden. Das ergibt den zweiten Teil der Definitionsmenge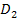 
. In diesem Fall überlappen sich der blaue und der rosafarbene Bereich jedoch nicht. Die Schnittmenge ist leer. Das ist auch logisch, denn es gibt keine Zahl, die größer ist als 2 und gleichzeitig kleiner ist als -2.
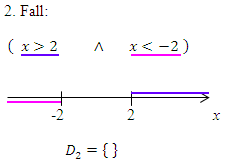
Um die Gesamtdefinitionsmenge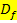 
zu erhalten, müssen normalerweise die beiden Teildefinitionsmengen 
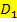und 
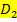vereinigt werden. Da hier jedoch 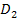die leere Menge ist, entspricht 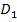direkt der Gesamtdefinitionsmenge 
.
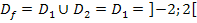
Die andere Schreibweise mit ℝ [...;...] ist hier nicht praktisch. Man müsste schließlich gleich zwei Bereiche ausschließen, nämlich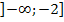 
und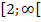 
. Diese Schreibweise wäre offensichtlich nicht kürzer, sondern umständlicher. Wir bleiben deshalb bei 
.
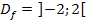2. Methode die quadratische Ungleichung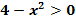 
zu lösen:Teils graphischer Weg
Schritt 1:
Wir ersetzen das Ungleichheitszeichen durch ein Gleichheitszeichen und lösen die so entstandene quadratische Gleichung nach x auf!
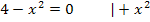
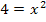
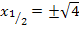
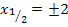
Achtung:Plus/Minus nicht vergessen! Wegen der geraden Potenz ergibt sich bei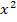 
die Zahl 4, sowohl wenn man +2 für x einsetzt als auch bei -2. Du darfst also keinesfalls die negative Lösung -2 übersehen!
Schritt 2:
Wir fassen die quadratische Gleichung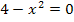 
als Nullstellenberechnung der Parabel 
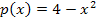auf. Wir kennen somit die Nullstellen der Parabel 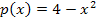. Sie liegen bei x = 2 und x = -2. Mit Hilfe der Nullstellen skizzieren wir die Parabel nun ganz grob. Es kommt dabei hauptsächlich darauf an, ob die Parabel nach oben oder nach unten geöffnet ist. Die Parabel 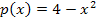ist nach unten geöffnet, weil vor dem 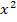ein Minus steht.
