Definitionsmenge ermitteln bei e- und ln- Funktionen
Wir kennen jetzt also die Nullstellen der Parabel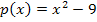 
. Sie liegen bei x = 3 und x = -3. Wir wollen nun die Parabel grob skizzieren. Die Parabel ist nach oben geöffnet, was man daran erkennt, dass vor dem 
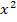praktisch ein Plus steht. (Bekanntlich sind für a >0 Funktionen der Form 
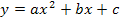nach oben geöffnete Parabeln. Für a <0 sind sie nach unten geöffnet. Mehr dazu bei:Parabeln zeichnen) Es handelt sich bei 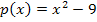um eine Normalparabel, da die Zahl vor dem 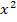hier gleich 1 ist. An sich spielt es jedoch für die Lösung der Ungleichung gar keine Rolle, wie breit die Parabel ist. Entscheidend ist ausschließlich, ob sie nach oben oder nach unten geöffnet ist. D.h. nur das Vorzeichen der Zahl vor dem 
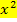ist entscheidend. Deine Skizze muss in diesem Fall also bloßirgendeine nach oben geöffnete Parabel mit den Nullstellen x = 3 und x = -3 zeigen;der Scheitel liegt natürlich genau in der Mitte von den beiden Nullstellen, hier also bei 
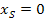. Auf die Breite der Parabel brauchst du also gar nicht so sehr zu achten.
So könnte deine Zeichnung aussehen:
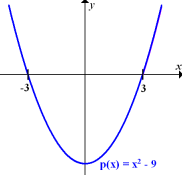
Abb.:Skizze der nach oben geöffneten Parabel 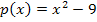mit ihren Nullstellen x = 3 und x = -3
Aus der Skizze lässt sich dann bequem ablesen, für welche Werte von x die Ungleichung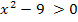 
erfüllt ist. Die Ungleichung lässt sich schließlich auch als 
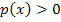schreiben, wobei 
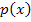für unsere Parabel steht. Das heißt anschaulich, dass wir diejenigen Zahlen x suchen, für die die Parabel 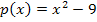oberhalb der x-Achse liegt. Du musst also schauen, wo die Parabel oberhalb der x-Achse verläuft und die entsprechenden Bereiche auf der x-Achse aus der Zeichnung ablesen. Das ergibt die Lösung der Ungleichung .
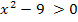Damit du besser verstehen kannst, wie das gemeint ist, sind in der folgenden Abbildung die entsprechenden Bereiche der Parabel hellblau markiert und die gesuchten Bereiche auf der x-Achse rot.
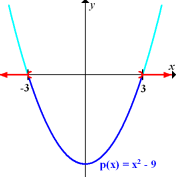
Abb.:Zur graphischen Lösung von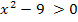
Aus der Zeichnung lesen wir jetzt die Bereiche auf der x-Achse ab, wo die Parabel oberhalb der x-Achse verläuft. (In der Abbildung auf der x-Achse rot markiert.)
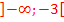sowie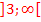 
Die Ungleichung 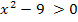ist somit erfüllt für alle Zahlen, die im Intervall 
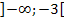oder im Intervall 
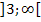liegen. Die beiden Intervalle müssen daher vereinigt werden. Dies ergibt die gesuchte Definitionsmenge der Funktion 
.
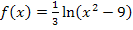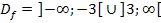
Stattdessen kann man natürlich auch folgendes schreiben:
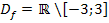
Diese Schreibweise haben wir oben bei der 1. Methode schon genauer besprochen.
