Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze
Vor den ersten beiden Logarithmen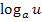 
und 
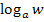steht jeweils ein positives Vorzeichen. Die Argumente u und w müssen also multipliziert werden. Vor dem letzten Logarithmus 
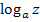steht ein Minus;daher muss beim zusammengefassten Logarithmus durch das Argument z dividiert werden. Z kommt daher in den Nenner.
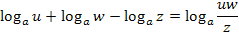
Vereinfachen lässt sich daran nichts mehr, also sind wir schon fertig.
Zu 3b.)
soll zu einem Logarithmus zusammengefasst und soweit möglich vereinfacht werden.
Bei dem ersten Logarithmus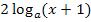 
verwenden wir das Logarithmus-Rechengesetz:
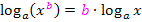
Das bedeutet, dass wir bei 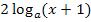die Zahl 2 als Exponent von 
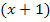schreiben dürfen. Wir wenden das Gesetz also rückwärts an: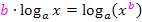 
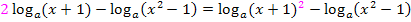
Als nächstes fassen wir beide Logarithmen zu einem einzigen Logarithmus zusammen. Weil vor dem hinteren Logarithmus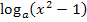 
ein Minus steht, kommt beim zusammengefassten Logarithmus der Ausdruck 
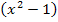in den Nenner. Vor dem ersten Logarithmus steht praktisch ein Plus;der Ausdruck 
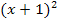kommt in den Zähler. Dabei verwendetes Logarithmus-Rechengesetz:
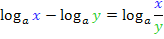
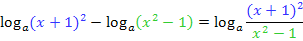
Was kann man als nächstes machen?
Bitte erst selbst kurz nachdenken!
Hast du es erkannt?
Richtig, im Nenner lässt sich jetzt die dritte binomische Formel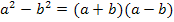 
anwenden, weil man sich 
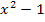auch als 
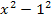denken kann.
Mit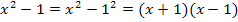 
ergibt sich:
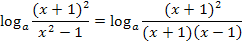
Jetzt weißt du bestimmt sofort, wie es weiter geht. Man kann natürlich kürzen mit (x + 1).
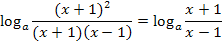
Fertig!
Hier noch einmal die komplette Rechnung:
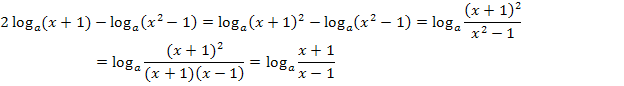
Zu 3c.)
Es soll der Ausdruck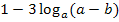 
zu einem Logarithmus zusammengefasst werden. Dazu muss erst einmal die Zahl 1 am Anfang des Ausdrucks als Logarithmus mit der Basis a geschrieben werden. (Bei 
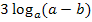kommt schließlich auch der Logarithmus zur Basis a vor und man kann nur Logarithmen mit der gleichen Basis zu einem Logarithmus zusammenfassen. Deshalb muss die Zahl 1 als Logarithmus zur Basis a geschrieben werden.) Bekanntlich gilt: 
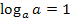(a hoch 1 ergibt schließlich 
.)
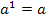Daraus folgt:
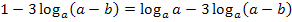
Die Zahl 3 vor dem zweiten Logarithmus schreiben wir in den Exponenten, d.h. wir wenden das folgende Rechengesetz an: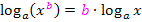
Wir wenden das Gesetz also rückwärts an: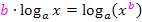
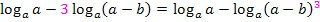
Nun fassen wir den Ausdruck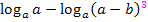 
zu einem Logarithmus zusammen. Vor dem zweiten Logarithmus steht ein Minus;deshalb kommt das Argument des zweiten Logarithmus 
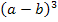beim zusammengefassten Logarithmus in den Nenner. Vor dem ersten Logarithmus steht quasi ein Plus;das Argument a kommt beim zusammengefassten Logarithmus in den Zähler des Bruchs. Wir wenden also das folgende Rechengesetz an:
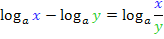
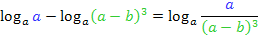
Weiter vereinfachen lässt hier nichts mehr. D.h. wir sind fertig!
