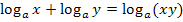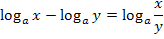Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze
Wir wenden also bei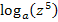 
das folgende Logarithmus-Rechengesetz an:
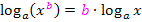
Entsprechend gilt:
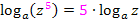
Damit folgt:
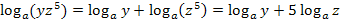
Fertig!
Zu 2d.)
Zu zerlegen: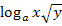 
Statt der Wurzel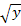 
wählen wir lieber die Potenzschreibweise 
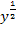. Dann gehen wir entsprechend vor wie bei Teilaufgabe 2c.
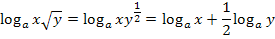
Zu 2e.)
Zu zerlegen: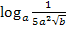 
Es werden dabei alle drei Logarithmus-Rechengesetze kombiniert angewendet. Bevor wir aber mit der Zerlegung des Logarithmus beginnen, schreiben wir die Wurzel als Potenz.
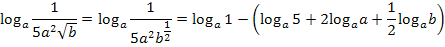
Mit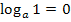 
und 
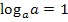ergibt sich:
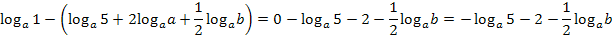
Zu 2f.)
Zu zerlegen: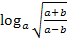 
Vorab schreiben wir die Wurzel wieder als Potenz.
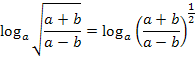
Nun lässt sich das Gesetz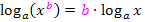 
anwenden. Wir ziehen also den Exponenten nach vorne vor den Logarithmus.
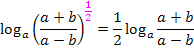
Da das Argument des vorliegenden Logarithmus ein Quotient ist, können wir außerdem das folgende Gesetz anwenden: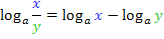 
Damit folgt:
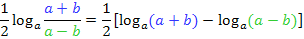
Achtung:Die eckige Klammer ist hier notwendig, da sich der Faktor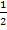 
auf beide Logarithmen beziehen muss. (Die Wurzel stand ursprünglich schließlich über dem gesamten Bruch!) Du kannst an statt der eckigen Klammer natürlich auch den Faktor 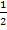vor jeden der beiden Logarithmen schreiben. Auch das nachfolgende Ergebnis ist korrekt.
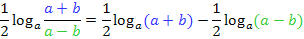
Sind wir nun endlich fertig oder kann man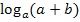 
bzw.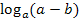 
noch weiter zerlegen?
Wir sind tatsächlich schon beim Endergebnis angelangt. Weder der Logarithmus 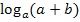noch der Logarithmus 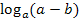lässt sich noch weiter zerlegen.
Vorsicht: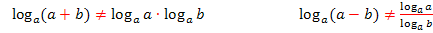 
Es gelten ausschließlich die folgenden Gesetze:
Bei 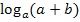und bei 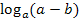kann man nicht mehr weiter rechnen! Du musst also ganz genau aufpassen! Ist das Argument des Logarithmus eine Summe oder Differenz, kann der Logarithmus nicht aufgeteilt werden! Nur bei Produkten oder Quotienten ist das möglich!
Hier noch einmal die gesamte Rechnung auf einen Blick:
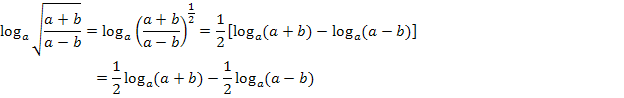
Bisher haben wir immer einen gegebenen Logarithmus in mehrere einzelne Logarithmen zerlegt. Um die Logarithmus-Rechengesetze noch etwas zu üben, machen wir das Ganze nun rückwärts. Wir wollen mehrere Logarithmen gleicher Basis zu einem einzigen der gleichen Basis zusammenfassen. Versuche die folgende Beispielaufgabe erst alleine und schau dir die Lösung nur zur Kontrolle an, oder wenn du nicht weiter weißt!
3. Bsp.:
Fasse folgende Ausdrücke jeweils zu einem einzigen Logarithmus zusammen und vereinfache soweit möglich!
a.)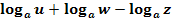 
b.)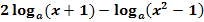 
c.)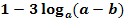 
Lösung:
Zu 3a.)
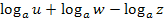soll zu einem Logarithmus zusammengefasst werden.
Wir verwenden dazu die beiden Rechengesetze:
