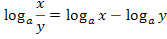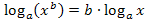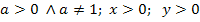Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze

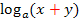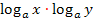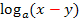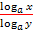Es reicht nämlich nicht, sich zu merken:„Aus plus wird mal und aus minus wird geteilt.“ „Aus plus wird mal“ könnte nämlich auch bedeuten, dass das gleiche ist wie . Das wäre aber falsch! Entsprechend könnte „aus minus wird geteilt“ bedeuten, dass und gleich sind. Aber auch das ist falsch!

Vorsicht: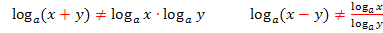

Die Ausdrücke 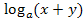und 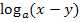 lassen sich nicht weiter umformen!

Es gelten für Logarithmen ausschließlich die folgenden Rechengesetze:

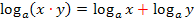
Dabei ist vorausgesetzt:

2. Bsp.:

Zerlege die folgenden Logarithmen, soweit möglich!

a.)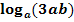

b.)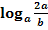

c.)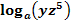

d.)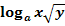

e.)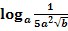

f.)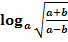

Lösung:

Zu 2a.)

Zu zerlegen: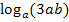

Das Argument 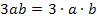ist ein Produkt, das aus den drei Faktoren 3, a und b besteht. Wir arbeiten deshalb mit dem Logarithmus-Rechengesetz:

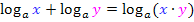
Allerdings verwenden wir dieses Gesetz in der umgekehrten Richtung:

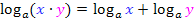
Damit ergibt sich:

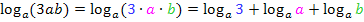
Den Ausdruck 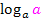kann man noch ausrechnen. Was kommt denn dabei heraus? Du musst dich fragen:„a hoch was ergibt a?“ Na klar, a hoch 1 ist wieder a! Deshalb gilt: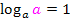

Das solltest du dir gut merken!

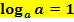
Damit ergibt sich:

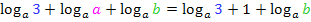
Die verbliebenen beiden Logarithmen lassen sich nicht weiter ausrechnen. D.h. wir sind fertig.

Hier noch einmal die gesamte Rechnung:

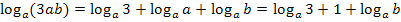
Zu 2b.)

Vollständig zu zerlegen ist der Ausdruck: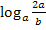

Das Argument 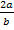ist ein Quotient. Mit dem folgenden Logarithmus-Rechengesetz lässt sich daher 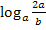zerlegen:

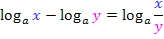
Wir brauchen das Gesetz aber genau umgekehrt:

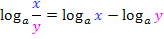
Bei dem vorliegenden Logarithmus 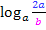steht 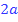im Zähler des Arguments und b im Nenner. Wenn wir den Logarithmus zerlegen, muss also vor 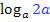quasi ein Plus stehen und vor 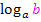ein Minus.

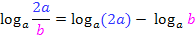
Sind wir damit schon am Ende der Rechnung? Nein! Der erste Logarithmus 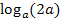kann nämlich noch weiter zerlegt werden! Das Argument 2a ist schließlich ein Produkt, bestehend aus den Faktoren 2 und a. Wir können deshalb auf 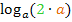das folgende Logarithmus-Rechengesetz anwenden:

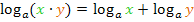
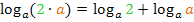
Damit folgt:

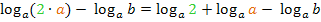
Wie in Teilaufgabe 2a.) schon besprochen gilt: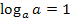

Somit erhalten wir als Endergebnis:

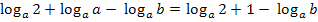
Die verbleibenden beiden Logarithmen lassen sich nicht weiter ausrechnen. Wir sind wirklich fertig.

Hier noch einmal die komplette Rechnung:

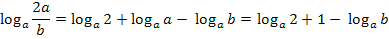
Zu 2c.)

Zu zerlegen: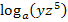

Das Argument 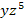ist ein Produkt. Daher können wir auf 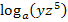das folgende Logarithmus-Rechengesetz anwenden:

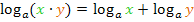
Damit ergibt sich:

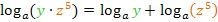
Bei dem zweiten Logarithmus 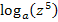lässt sich noch die Potenz vor den Logarithmus ziehen.

---