Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze

(Der Exponentenvergleich klappt ja nur dann, wenn auf beiden Seiten der Gleichung dieselbe Basis steht.) Bekanntlich gilt: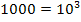

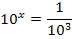
Jetzt ziehen wir 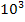noch in den Zähler, indem wir das Vorzeichen des Exponenten umdrehen. (Vergleiche das Potenzgesetz: )

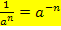Merke:Willst du einen Ausdruck vom Nenner in den Zähler hochziehen (oder umgekehrt vom Zähler in den Nenner hinunterschieben), musst du nur das Vorzeichen des Exponenten umdrehen. Wir nennen dieses Prinzip etwas flappsig „Aufzugfahren“. Immer wenn du einen Term vom Zähler in den Nenner oder umgekehrt vom Nenner in den Zähler, also bei einem Bruch rauf oder runter schieben willst, musst du das Vorzeichen des Exponenten umdrehen.

Beim „Aufzugfahren“ immer das Vorzeichen des Exponenten umdrehen!

Auf der rechten Seite unserer Gleichung tun wir jetzt also „Aufzugfahren“.

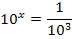
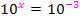
Durch Exponentenvergleich erhalten wir die Lösung:

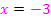
Daraus folgt: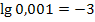

Tipp:Bei Stufenzahlen, wie z.B. 10;100;1000 oder 0,1;0,01;0,001 etc., lässt sich der Zehner-Logarithmus ganz leicht im Kopf berechnen. Man muss nur die Anzahl der Nullen zählen, die hinter bzw. vor der 1 stehen. Die Anzahl der Nullen ist schon das Ergebnis. (Bei Kommazahlen muss die Null vor dem Komma mitgezählt werden, das Ergebnis ist dann außerdem negativ.)

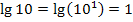
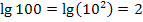
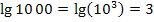
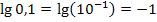
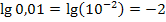
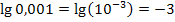
Zu 1f.)

Gesucht: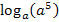

Wir müssen uns also fragen:„a hoch was ergibt 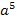?“ Na klar, a hoch 5 ergibt 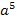. Die Lösung ist somit einfach die Zahl 5.

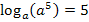
Allgemein gilt auch: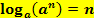

Z.B.: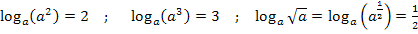

Zu 1g.)

Gesucht: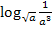

Wir können diesen Logarithmus wieder über die zugehörige Exponentialgleichung ausrechnen.

Wir fragen uns:„ 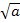hoch was ergibt ?“

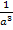Zugehörige Exponentialgleichung:

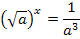
Wir schreiben die Wurzel 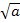als Potenz :

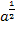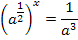
Wir verwenden auf der linken Seite der Gleichung das Potenzgesetz: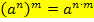

Auf der rechten Seite der Gleichung arbeiten wir nun mit dem Potenzgesetz: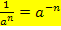

Auf der rechten Seite wenden wir also das Prinzip „Aufzugfahren“ an. (Vergleiche dazu Teilaufgabe 1e!)

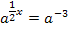
Nach Anwendung der erwähnten Potenzgesetze steht auf beiden Seiten der Gleichung dieselbe Basis und wir können einen Exponentenvergleich machen. Daraus ergibt sich:

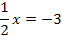
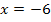
Somit kennen wir die Lösung: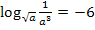

Nun weißt du hoffentlich, was ein Logarithmus eigentlich überhaupt ist. Wichtig sind außerdem noch die Rechengesetze für Logarithmen.

Logarithmus-Rechengesetze:

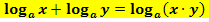
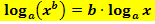
Anmerkung:Diese Rechengesetze für Logarithmen stehen auch in deiner Formelsammlung bzw. Merkhilfe. Dennoch solltest du sie besser auswendig wissen. Wenn du dir allerdings unsicher bist, auf welcher Seite z.B. bei der ersten Formel „plus“ und auf welcher Seite „mal“ steht, besser nachschauen.

---