Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze

Bei Gleichungen der Form 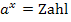nimmt man den Logarithmus zur Basis a , also 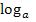, um nach dem Exponenten x aufzulösen.

Nach dem Exponenten löst man auf mit dem Logarithmus zur entsprechenden Basis!

Allgemein gilt also für beliebige a >0, 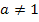und b >0:

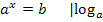
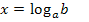
Bsp.:

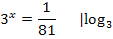
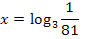
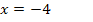
Achtung:Logarithmus und Wurzel nicht durcheinander bringen!

Muss (im Gegensatz zum soeben gezeigten Beispiel) jedoch eine Gleichung der Form 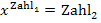nach x aufgelöst werden, darf nicht der Logarithmus verwendet werden, sondern es muss dabei die entsprechende Wurzel gezogen werden. Soll z. B. die Gleichung 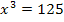nach x aufgelöst werden, braucht man die dritte Wurzel .

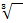Ist also bei einer Gleichung x die Basis, d.h. x steht unten und nicht oben im Exponenten, und man soll nach x auflösen, nimmt man die entsprechende Wurzel. (Bei 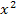die zweite Wurzel, also die „normale“ Wurzel 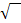, bei 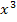die dritte Wurzel 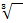, bei 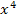die vierte Wurzel 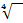usw., allgemein bei 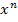die n.te Wurzel .)

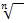Nach der Basis löst man auf mit der n.ten Wurzel.

Allgemein gilt also für beliebige reelle 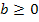und n ℕ :

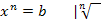
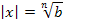
Für gerade n ergeben sich dabei zwei Lösungen: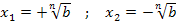

Für ungerade n ergibt sich nur eine Lösung: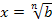

Mehr dazu im gesonderten Kapitel:n.-te Wurzel

Logarithmen ohne Taschenrechner berechnen:

Wie kann man einen angegebenen Logarithmus der Form 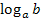, also z. B. 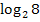, ohne Taschenrechner ausrechnen?

Dazu muss man die zugehörige Exponentialgleichung 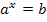lösen.

Bei 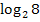ist das die Gleichung 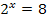. Man fragt sich also:„2 hoch was ergibt 8“? Dies ist gleichbedeutend mit der Frage:„Wie oft muss man die Zahl 2 mit sich selbst multiplizieren, bis sich die Zahl 8 ergibt?“ Du weißt natürlich: 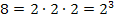Deshalb ergibt sich: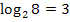

Leider geht das nicht bei allen Logarithmen so einfach, wie bei 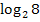. Wie auch schwierigere Logarithmen ohne Taschenrechner ausgerechnet werden, wird gleich an Hand der Aufgaben des 1. Beispiels erklärt. Vorweg halten wir jedoch schon mal das Wichtigste fest:

Um das Ergebnis eines Logarithmus der Form 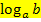zu finden, muss du dich fragen:„a hoch was ergibt b?“

Der Logarithmus 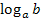ist also die Lösung der Exponentialgleichung 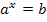. Die Exponentialgleichung 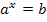hat für 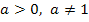und 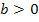die Lösung .

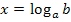1. Bsp.:

Berechne die folgenden Logarithmen ohne Taschenrechner! (Bei den beiden letzten Teilaufgaben 1f. und 1g. geht es sowieso nicht anders, weil man schließlich kein a in den Taschenrechner eingeben kann.)

a.)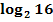

b.)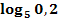

c.)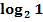

d.)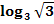

e.)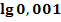

f.)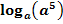

g.)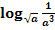

Lösung:

Zu 1a.

---