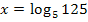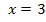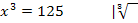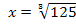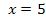Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze

Ältere Taschenrechner haben jedoch oft nur die Tasten  log (Zehner-Logarithmus) und  ln  (natürlicher Logarithmus), aber keine Taste für Logarithmen zu einer anderen Basis. Du musst dann einen kleinen Trick anwenden, um auch Logarithmen zu beliebigen Basen mit diesem Taschenrechner ausrechnen zu können:Mit dem Rechengesetz 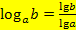bzw. in der Taschenrechnerschreibweise 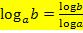lässt sich jeder Logarithmus ausrechnen. Anstatt des Zehner-Logarithmus lg bzw. log kannst du auch den ln verwenden;dabei kommt ebenfalls das Richtige heraus. Es gilt also auch: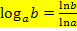

(Die Beweise dieser Gesetze sparen wir uns, weil du sie sowieso nicht brauchst. Du musst nur wissen, dass die erwähnten Rechengesetze gelten.)

Rechne statt 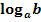einfach 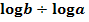oder !

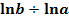Beispielsweise statt 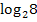einfach 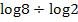oder 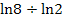eintippen und schon ist das Problem gelöst. Probiere das gleich mal selbst mit deinem Taschenrechner aus. Es muss jeweils das Ergebnis 3 herauskommen.

Und gleich noch einmal zur Übung für alle Schüler, die noch einen älteren Taschenrechner ohne 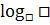   -Taste benützen:Was ergibt beispielsweise 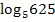und wie rechnest du das mit deinem Taschenrechner aus, der nur die Tasten  log  und  ln  besitzt?

Hast du das inzwischen selbst mit deinem Taschenrechner ausgerechnet? Ok, dann müsstest du auf das Ergebnis 4 gekommen sein. Um 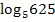zu berechnen, hast du dann Folgendes eingetippt: 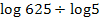oder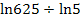

Jetzt weißt du hoffentlich, wie man Logarithmen mit dem Taschenrechner ausrechnet und wann du überhaupt einen Logarithmus brauchst.

Wir halten noch einmal fest:

Man verwendet einen Logarithmus, um eine Gleichung mit x im Exponenten nach x aufzulösen! Der Logarithmus ist nur für positive Argumente definiert.

Vorsicht:Nicht verwechseln mit der n.ten Wurzel 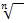! Eine Wurzel verwendest du nur dann, wenn du eine Gleichung lösen sollst, wobei x die Basis bildet und der Exponent eine richtige Zahl ist!

Zum Unterschied zwischen Logarithmus und Wurzel:

Exponent gesucht: Logarithmus

Basis gesucht: n.te Wurzel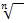

Steht bei einer Gleichung x oben, also im Exponenten, nimmt man den entsprechenden Logarithmus.

Bei Gleichungen der Form 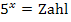braucht man 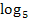, sprich „Fünferlogarithmus“ oder „Logarithmus zur Basis Fünf“, um nach dem x aufzulösen, das im Exponenten steht.

Bei Gleichungen mit 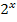nimmt man entsprechend 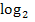, sprich „Zweierlogarithmus“ oder „Logarithmus zur Basis Zwei“. Bei 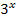nimmt man dann 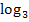, sprich „Logarithmus zur Basis Drei“;bei 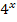den Logarithmus zur Basis Vier .

---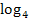