Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze
(Die Schreibweisen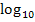 
und lg bedeuten beide dasselbe;in manchen Büchern und auf dem Taschenrechner steht für den Zehner-Logarithmus auch nur log , ganz ohne hingeschriebener Basis. 
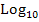, lg und log stehen also alle für den Zehner-Logarithmus. Wir verwenden auf dieser website ab sofort nur noch die Schreibweise lg für den Zehner-Logarithmus.)
Du kannst die oben gezeigten Gleichungen also auch alle mit einem Logarithmus lösen. Das geht folgendermaßen:
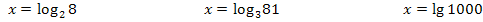
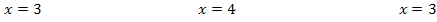
Die Zahl, auf die sich der Logarithmus jeweils bezieht, die also großgeschrieben direkt hinter log steht, wird als Argument des Logarithmus bezeichnet. Das Argument des Logarithmus muss grundsätzlich positiv sein! Ansonsten ist der Logarithmus nicht definiert! Die Basis (bei log kleiner und tiefergestellte Zahl) ist laut Definition ebenfalls positiv und ungleich 1.(Dass die Basis immer positiv sein soll, wurde einfach so festgelegt. Das ist eben so. Die Zahl 1 als Basis wäre nicht sinnvoll, denn die Gleichung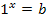 
wäre nur lösbar für b = 1 und dann ist sie für beliebige reelle x erfüllt. 
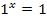ist schließlich immer erfüllt.)
Beispielsweise wäre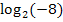 
nicht definiert, weil das Argument -8 negativ ist! Die zugehörige Exponentialgleichung 
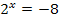hat keine Lösung, da die positive Zahl 2 potenziert niemals die negative Zahl 8 ergeben kann. Eine positive Zahl kann potenziert niemals etwas Negatives ergeben. Daher darf das Argument des Logarithmus niemals negativ sein. Das Argument darf auch nicht gleich Null sein, denn eine positive Zahl kann potenziert nicht negativ werden.
Bei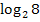 
ist beispielsweise die Basis die positive Zahl 2 und das Argument die positive Zahl 8, deshalb ist 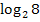definiert.
Kleiner Test, ob du es verstanden hast:Was ist zum Beispiel bei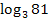 
die Basis und was das Argument? Ist dieser Logarithmus definiert und warum?
Na klar, die Zahl 3 ist die Basis und 81 ist das Argument. Weil Basis und Argument positiv sind, ist 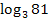definiert.
Entsprechend ist bei lg1000 die Zahl 1000 das Argument. Die Basis ist die Zahl 10, weil lg1000 nur eine andere Schreibweise für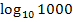 
ist. Basis und Argument sind positiv und daher ist lg1000 logischerweise definiert.
Hinweise zur Berechnung von Logarithmen der allgemeinen Basis a mit dem Taschenrechner:
Modernere Taschenrechnermodelle haben zusätzlich zu den Tasten log (Zehner-Logarithmus) und ln auch noch eine Taste für Logarithmen zu einer beliebigen Basis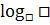 
. (ln steht für den natürlichen Logarithmus, das ist der Logarithmus zur Basis e, zu dem kommen wir erst später. Siehe unten!), Mit diesen Taschenrechnermodellen ist es ganz leicht jegliche Logarithmen zu berechnen.
