Kurzwiederholung des Logarithmus (zur allgemeinen Basis a) inklusive log-Rechengesetze
Stelle dir vor, dass du irgendeine Gleichung mit x im Exponenten lösen sollst. Zum Beispiel eine der folgenden Gleichungen:
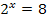
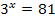
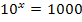
Wie gehst du da vor? Versuche jetzt nur durch Überlegung auf die Lösungen dieser drei Gleichungen zu kommen! (Die Zahlen sind absichtlich einfach gewählt;daher schaffst du das bestimmt.)
Hast du dir die Lösungen inzwischen selbständig überlegt? Ja? Ok, dann zu deiner Kontrolle hier die Lösungen:
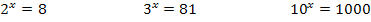
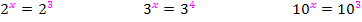
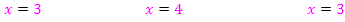
Soweit müsste noch alles klar sein. Was du da gerade im Kopf gemacht hast, war schon der Logarithmus! Bei der Gleichung 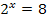hast du den Logarithmus zur Basis 2 (kurz Zweier-Logarithmus genannt) 
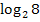berechnet. Bei der Gleichung 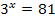hast du den Logarithmus zur Basis 3 (kurz Dreier-Logarithmus) 
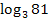berechnet und bei der letzten Gleichung 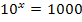entsprechend den Logarithmus zur Basis 10, also den Zehner-Logarithmus, 
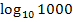berechnet. (Statt 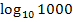kann man auch 
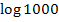schreiben oder 
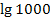;das sind nur andere Schreibweisen. 
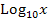ist das gleiche wie 
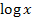oder 
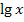. Log oder lg sind abgekürzte Schreibweisen für den Zehner-Logarithmus, d.h. ausschließlich für den Logarithmus zur Basis Zehn, also für 
. Wir werden hier auf dieser website für den Zehner-Logarithmus die Schreibweise lg verwenden und nicht log, wie es auf dem Taschenrechner steht.)
Noch einmal ganz langsam:
Was genau bedeutet 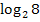(sprich:„Logarithmus von 8 zur Basis 2“)? Ganz einfach:Man muss sich überlegen, mit welcher Zahl x man die Basis 2 potenzieren muss, um auf das Ergebnis 8 zu kommen. Du fragst dich also:„2 hoch was ergibt 8?“ Wir haben uns vorher schon überlegt, dass 2 hoch 3 genau 8 ergibt. Daher ist die Zahl 
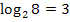. Du kannst umgekehrt überprüfen, ob 
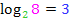korrekt ist, indem du schaust, ob 
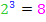gilt. (Natürlich stimmt das.)
In anderen Worten der Logarithmus zur Basis 2 (Zweier-Logarithmus) holt bei der Gleichung 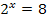das x aus der Potenz herunter. Mit dem Zweier-Logarithmus kannst du die Gleichung 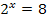nach x auflösen. Man braucht den Logarithmus zur Basis 2, also 
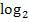, weil in der Gleichung 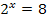die Basis (die Zahl, die beim x unten steht) 2 ist.
Entsprechend braucht man bei der Gleichung 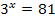den Logarithmus zur Basis 3 (Dreier-Logarithmus) 
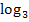, um nach x aufzulösen. Bei der Gleichung 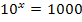braucht man dann den Logarithmus zur Basis 10 (Zehner-Logarithmus) 
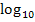oder lg , um nach x aufzulösen.
