Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze

Einsetzen in die Mitternachtsformel ergibt dann:

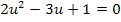
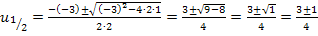
Nun wissen wir zwar, was u ist, aber noch nicht was x ist. Um heraus zu finden, was die ursprüngliche Variable x ist, setzen wir nacheinander die berechneten Werte von u in die Gleichung 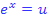ein und lösen jeweils nach x auf.

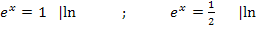
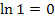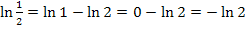Mit und ergeben sich die Lösungen:

Hinweis:

Die Lösungen einer Gleichung der Form 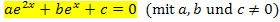werden immer durch die Substitution 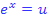und anschließender Verwendung der Mitternachtsformel berechnet.

Entsprechend können Gleichungen der Form 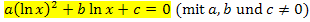durch die Substitution 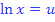und anschließender Verwendung der Mitternachtsformel gelöst werden. (Vergleiche nächste Teilaufgabe!)

Zu 4g.)

Hier noch einmal die Gleichung: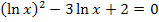

Definitionsmenge:D =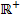

Hinweis:Der lnx ist wie alle Logarithmen nur für positive Argumente x definiert.

Ähnlich wie in Teilaufgabe 4f. hilft auch bei dieser Gleichung eine Substitution. Wir ersetzen hier den Ausdruck lnx durch die neue Variable u.

Substitution:lnx = u

Dadurch ergibt sich wieder eine gemischtquadratische Gleichung, die wir mit der Mitternachtsformel nach u auflösen können. Danach erfolgt dann die Rücksubstitution, d.h. wir setzen die berechneten Werte für u in lnx = u ein und lösen nach x auf.

Am besten ist es, wenn du das erst einmal alleine versuchst, bevor du dir den Rest der Lösung anschaust.

Hoffentlich hast du es inzwischen selbst gerechnet, wenn nicht dann jetzt!

Ok, dann hier die komplette Lösung:

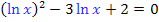
Substitution :lnx = u

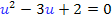
Mit der Mitternachtsformel erhält man:

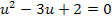
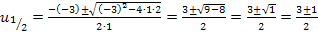
Rücksubstitution:

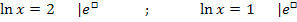
Beide ermittelten Werte 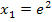und 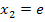sind positiv und liegen daher innerhalb der Definitionsmenge D = 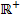. (Du weißt: 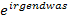ist immer positiv!) Daher gehören beide Werte zur Lösungsmenge der Gleichung.

Die Lösungen lauten somit: 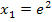und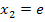

Dies soll uns an dieser Stelle zu Gleichungen mit 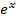und lnx reichen. Bei der Kurvendiskussion von schwierigeren e-Funktionen bzw. schwierigeren ln-Funktionen werden noch weitere Beispiele gezeigt, wobei ähnliche Gleichungen gelöst werden müssen. Bei der Berechnung der Nullstellen und Extrema von e- oder ln-Funktionen wirst du immer wieder mit solchen Gleichungen konfrontiert werden. Daher musst du derartige Gleichungen unbedingt lösen können!

Nun aber zu einer anderen Frage:Wie kann man den ln ohne Taschenrechner im Kopf ausrechnen? Geht das überhaupt?

Im Kopf ausrechnen kann man den ln nur in ganz bestimmten Sonderfällen.

Merke: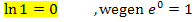

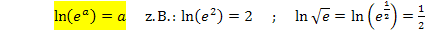
Umgekehrt gilt auch:

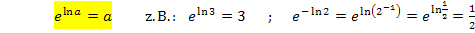
Wie wir bei den Gleichungen mit 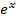und lnx schon gelernt haben, heben sich der ln und 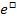gegenseitig auf – aber eben nur dann, wenn sie direkt nacheinander angewendet werden. Das ist praktisch genauso wie bei Wurzel 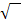und Quadrat 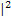oder bei dritter Wurzel 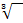und hoch Drei 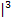;die heben sich auch jeweils wieder gegenseitig auf. Das liegt daran, dass die Funktionen 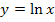und 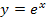Umkehrfunktionen zueinander sind, genauso wie 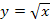und 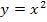bzw. wie 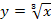und 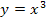. Daher führen wir nun gleich die ln-Funktion ein. Eben diese Funktion ist es, die für uns von Relevanz ist.

---