Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze

Es handelt sich hierbei offensichtlich um eine Exponentialgleichung, da x im Exponenten steht. Jetzt kommt aber nicht nur 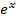sondern auch 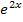in der Gleichung vor. Was tun? Überlege doch erst mal alleine!

Keine Idee?

Kleiner Tipp:Ausklammern hilft!

Bist du jetzt selbst darauf gekommen? Es lässt sich hier leicht 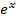ausklammern und dadurch entsteht mal wieder eine Gleichung der Form „Produkt gleich Null“. Dass man dann die Faktoren einzeln gleich Null setzen darf, ist dir inzwischen bestimmt klar. Also los geht´s! Gleich mal selbst probieren, bevor du den Rest der Lösung anschaust.

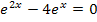
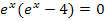
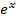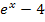Nun müssten an sich die Faktoren und einzeln gleich Null gesetzt werden. Da 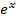bekanntlich aber immer positiv ist, kann 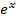nicht gleich Null sein. Du schreibst einfach 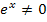oder 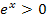und setzt dann nur noch den zweiten Faktor 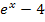gleich Null. Das sieht dann folgendermaßen aus:

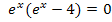
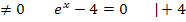
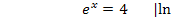
Das Ergebnis ln4 können wir noch etwas „verschönern“, indem wir die 4 als 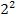schreiben und das dritte ln-Rechengesetz anwenden, d.h. den Exponenten vor den ln ziehen. Das ist natürlich reine „Kosmetik“, doch oft gibt es darauf in Prüfungen noch einen Punkt.

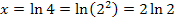
Fertig!

Zu 4f.)

Hier noch einmal die zu lösende Gleichung: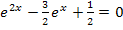

Jetzt ergibt sich ein neues Problem:Das x kommt bei 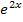und bei 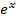im Exponenten vor, aber ausklammern lässt sich 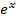wegen der Zahl 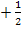nicht. Hm?

Hast du eine Idee? Nein? Ok, dann eine kleine Hilfe:

Mit dem Potenzgesetz 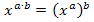lässt sich 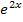umformen:

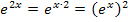
Damit ergibt sich:

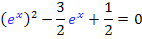
In dieser Form ist es leichter zu erkennen, dass die folgende Substitution gemacht werden kann:

Substitution: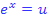

Das bedeutet:Wir ersetzen den Ausdruck 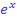durch die neue Variable u. Dadurch ergibt sich die folgende Gleichung mit der Variablen u.

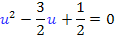
Dies ist eine gemischtquadratische Gleichung, also eine Gleichung mit 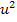und u. Sie lässt sich mit der Mitternachtsformel lösen. Bevor wir in die Mitternachtsformel einsetzen multiplizieren wir die Gleichung aber noch mit dem Hauptnenner der Brüche, also mit der Zahl 2. Dadurch fallen nämlich praktischerweise alle Brüche weg und ohne Brüche rechnet es sich einfach bequemer. (Du kannst natürlich auch einfach mit den Brüchen rechnen, dann musst du nicht vorher mit 2 durchmultiplizieren.)

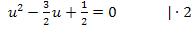
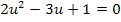
Zur Erinnerung hier noch einmal die Mitternachtsformel:

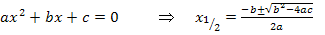
Statt 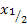schreiben wir dabei natürlich 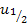, da wir schließlich momentan eine Gleichung mit der Variablen u zu lösen haben.

---