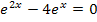Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze
Das liegt daran, dass man bei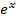 
beliebige reelle Zahlen für x einsetzen kann. Für reine Exponentialgleichungen (Gleichungen mit x im Exponenten, aber ohne Logarithmus, ohne Wurzel oder x im Nenner) gilt allgemein:D = ℝ
Wie löst man diese Gleichung nun aber nach x auf? Hast du selbst eine Idee?
Die vorliegende Gleichung hat, wie die Gleichung in Teilaufgabe 4c., die Form „Produkt gleich Null“. Wir setzen also die Faktoren des Produkts einzeln gleich Null. Die entstehenden Teilgleichungen lösen wir dann getrennt nach x auf.
Der erste Faktor ist eigentlich die Konstante (d.h. Zahl ohne x)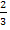 
und das kann gar nicht gleich Null werden;wir können 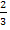einfach ignorieren bzw. weglassen. Dem Weglassen von 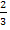entspricht auch die Division der gesamten Gleichung durch 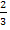oder die Multiplikation mit dem Kehrwert 
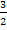. Wegen 
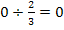bzw. 
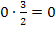ändert sich an der Zahl 0 auf der rechten Seite der Gleichung nichts;es fällt nur die Zahl 
auf der linken Seite weg.
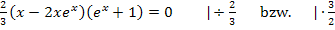
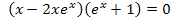
Faktoren / Klammern einzeln gleich Null setzen:
Bei der ersten Gleichung klammern wir x aus;dadurch ergibt sich wieder eine Gleichung der Form „Produkt gleich Null“. (Wir setzen dann nachher wieder die einzelnen Faktoren gleich Null.)
Bei der zweiten Gleichung isolieren wir vorweg den Ausdruck 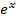;wir bringen also die 1 auf die andere Seite. Dann sehen wir weiter.
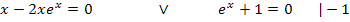
Die erste Gleichung hat nun die Form „Produkt gleich Null“, wir setzen wieder die einzelnen Faktoren gleich Null.
Die zweite Gleichung hat die Form „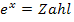 
“, wir müssten jetzt eigentlich den ln anwenden, um nach dem Exponenten x aufzulösen. Der ln von negativen Zahlen ist jedoch gar nicht definiert. Wie du weißt, ist 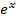immer positiv und kann gar nichts Negatives ergeben. Somit kann die Gleichung 
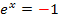keine Lösung haben!
Dass die zweite Teilgleichung keine Lösung hat, hätte man an sich schon bei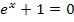 
erkennen können:Weil 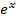alleine schon positiv, also größer als Null ist, muss 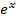+ eine Zahl und somit auch 
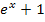erst recht größer als Null sein. 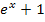kann also überhaupt nicht gleich Null sein. Damit ist die Aussage 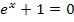einfach falsch! Es liegt ein Wiederspruch in sich vor. Daraus folgt:Es gibt kein x, das die Gleichung 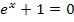erfüllen könnte.
Demnach können die einzigen Lösungen von der ersten Teilgleichung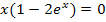 
kommen.
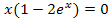
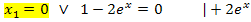
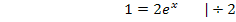
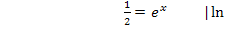
Das Ergebnis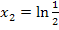 
lässt sich noch umformen:
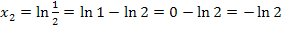
Nun haben wir alle Lösungen der gegebenen Gleichung ermittelt.
Sie lauten: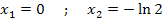 
Zu 4e.)
Hier noch einmal die Angabe: 
